题目内容
4.(1)计算:-14+$\sqrt{12}$sin60°+($\frac{1}{2}$)-2-(π-$\sqrt{5}$)0(2)先化简,再求值:(1-$\frac{1}{x+2}$)÷$\frac{{x}^{2}+2x+1}{x+2}$,其中x=$\sqrt{3}$-1.
分析 (1)根据实数的运算法则计算即可;
(2)原式利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
解答 解:(1)-14+$\sqrt{12}$sin60°+($\frac{1}{2}$)-2-(π-$\sqrt{5}$)0=-1+2$\sqrt{3}$×$\frac{\sqrt{3}}{2}$+4-1=5;
(2)(1-$\frac{1}{x+2}$)÷$\frac{{x}^{2}+2x+1}{x+2}$=$\frac{x+2-1}{x+2}$×$\frac{x+2}{(x+1)^{2}}$=$\frac{1}{x+1}$,
当x=$\sqrt{3}$-1时,
原式=$\frac{\sqrt{3}}{3}$.
点评 此题考查了实数的运算,分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
9. 如图是一个空心圆柱体,它的左视图是( )
如图是一个空心圆柱体,它的左视图是( )
 如图是一个空心圆柱体,它的左视图是( )
如图是一个空心圆柱体,它的左视图是( )| A. |  | B. |  | C. |  | D. |  |
13. 如图,在矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AC=6cm,则AB的长是( )
如图,在矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AC=6cm,则AB的长是( )
 如图,在矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AC=6cm,则AB的长是( )
如图,在矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AC=6cm,则AB的长是( )| A. | 3cm | B. | 6cm | C. | 10cm | D. | 12cm |
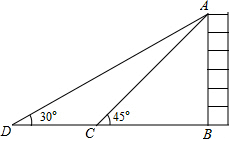 如图所示,为了测量出一垂直水平地面的某高大建筑物AB的高度,一测量人员在该建筑物附近C处,测得建筑物顶端A处的仰角大小为45°,随后沿直线BC向前走了100米后到达D处,在D处测得A处的仰角大小为30°,则建筑物AB的高度约为137米.
如图所示,为了测量出一垂直水平地面的某高大建筑物AB的高度,一测量人员在该建筑物附近C处,测得建筑物顶端A处的仰角大小为45°,随后沿直线BC向前走了100米后到达D处,在D处测得A处的仰角大小为30°,则建筑物AB的高度约为137米. 如图所示,C城市在A城市正东方向,现计划在A、C两城市间修建一条高速公路(即线段AC),经测量,森林保护区的中心P在A城市的北偏东60°方向上,在线段AC上距A城市120km的B处测得P在北偏东30°方向上,已知森林保护区是以点P为圆心,100km为半径的圆形区域,请问计划修建的这条高速公路是否穿越保护区,为什么?(参考数据:$\sqrt{3}$≈1.73)
如图所示,C城市在A城市正东方向,现计划在A、C两城市间修建一条高速公路(即线段AC),经测量,森林保护区的中心P在A城市的北偏东60°方向上,在线段AC上距A城市120km的B处测得P在北偏东30°方向上,已知森林保护区是以点P为圆心,100km为半径的圆形区域,请问计划修建的这条高速公路是否穿越保护区,为什么?(参考数据:$\sqrt{3}$≈1.73)
 尺规作图(不写作法,保留作图痕迹):
尺规作图(不写作法,保留作图痕迹):