题目内容
对于边长为3、4、5的三角形，存在一个面积最小的正方形，恰好将这个三角形覆盖，那么这个正方形的面积为 ．
考点：勾股定理,正方形的性质
专题：
分析：作出图形，设正方形的边长为x，根据勾股定理表示出BE、DF，再表示出AE、AF，然后利用勾股定理列出方程求解即可．
解答：
解：设正方形的边长为x，
由勾股定理得，BE=
，DF=
，
所以AE=AB-BE=x-
，AF=AD-DF=x-
，
在Rt△AEF中，EF2=AF2+AE2，
即32=（x2+（x-
）2，
整理得，x（
+
）=16，
解得x=
．
故答案为：
．
解：设正方形的边长为x，由勾股定理得，BE=
| 16-x2 |
| 25-x2 |
所以AE=AB-BE=x-
| 16-x2 |
| 25-x2 |
在Rt△AEF中，EF2=AF2+AE2，
即32=（x2+（x-
| 16-x2 |
整理得，x（
| 16-x2 |
| 25-x2 |
解得x=
16
| ||
| 17 |
故答案为：
16
| ||
| 17 |
点评：本题考查了勾股定理，正方形的性质，熟记性质与定理并列出方程是解题的关键，作出图形更形象直观．
练习册系列答案
相关题目
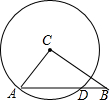如图，在⊙C中，CA⊥CB，且CA=3，CB=4，求AD的长．
如图，△ABC中，已知BD=3CD，AM=2DM．求
若从圆锥形纸帽的底面圆周上点A处用一条红线绕纸帽的侧面一圈，那么这样的红线至少要