题目内容
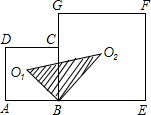如图，边长为a的正方形ABCD和边长为b的正方形BEFG排放在一起，O1和O2分别是两个正方形的中心，则阴影部分的面积为分析：阴影部分的面积可以看成两个三角形面积之和，所以求2个三角形面积即可；线段O1O2的长根据勾股定理求解．
解答：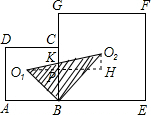
解：做O1H∥AE，使O2H⊥O1H，交BG于P，K点，
（1）BP=
a，
又∵O2H⊥HO1，
∴KP∥HO2，
∴△PKO1∽△HO2O1，
∴
=
=
，
KP=
×
=
，
阴影部分的面积=
×BK×（
）=
×[
+
]×
=
=
；
（2）HO1=
，HO2=
，
根据勾股定理O1O2=
=
=
．
故答案为：
；
．
解：做O1H∥AE，使O2H⊥O1H，交BG于P，K点，（1）BP=
| 1 |
| 2 |
又∵O2H⊥HO1，
∴KP∥HO2，
∴△PKO1∽△HO2O1，
∴
| KP |
| HO2 |
| PO1 |
| HO1 |
| a |
| a+b |
KP=
| a |
| a+b |
| b-a |
| 2 |
| ab-a2 |
| 2(a+b) |
阴影部分的面积=
| 1 |
| 2 |
| a+b |
| 2 |
| 1 |
| 2 |
| a |
| 2 |
| ab-a2 |
| 2(a+b) |
| a+b |
| 2 |
=
| 2ab |
| 8 |
| ab |
| 4 |
（2）HO1=
| a+b |
| 2 |
| b-a |
| 2 |
根据勾股定理O1O2=
| HO12+HO22 |
=
|
=
| 1 |
| 2 |
| 2(a2+ b2) |
故答案为：
| ab |
| 4 |
| 1 |
| 2 |
| 2(a2+ b2) |
点评：本题考查的相似三角形的证明即对应边比例相等的性质，三角形面积的计算，考查了根据勾股定理计算直角三角形斜边的应用，解决本题的关键是构建直角三角形HO1O2．
练习册系列答案
相关题目
如图，边长为6的正方OABC的顶点O在坐标原点处，点A、C分别在x轴、y轴的正半轴上，点E是OA边上的点（不与点A重合），EF⊥CE，且与正方形外角平分线AC交于点P．
如图，边长为6的正方OABC的顶点O在坐标原点处，点A、C分别在x轴、y轴的正半轴上，点E是OA边上的点（不与点A重合），EF⊥CE，且与正方形外角平分线AC交于点P．
轴正方向连续翻转2006次，点P依次落在点
，
，
，
，……
的位置，则
＝_________．
