题目内容
若x+y=12，求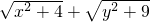
的最小值________．
13
分析：将x+y=12变形后代入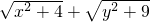，再转化为轴对称最短路径问题解答即可．
解答：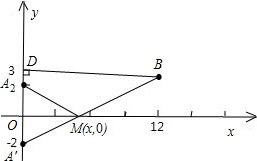
解：∵x+y=12，
∴y=12-x①，
将①代入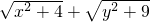得，
②，
由②得，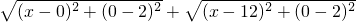
，
可理解为M（x，0）到A（0，2）和B（12，3）的距离的最小值．
作A关于轴的对称点A'（0，-2），连接A′B，与x轴交点即为M．
在Rt△A'DB中，A'B=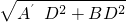
=
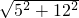=13．
故答案为：13．
如图：
点评：此题考查了利用两点间距离公式的几何意义解答最值问题，体现了数形结合思想的重要作用．
分析：将x+y=12变形后代入
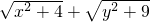，再转化为轴对称最短路径问题解答即可．解答：
解：∵x+y=12，∴y=12-x①，
将①代入
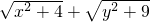得，②，由②得，
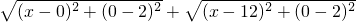，可理解为M（x，0）到A（0，2）和B（12，3）的距离的最小值．
作A关于轴的对称点A'（0，-2），连接A′B，与x轴交点即为M．
在Rt△A'DB中，A'B=
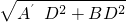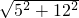==13．故答案为：13．
如图：
点评：此题考查了利用两点间距离公式的几何意义解答最值问题，体现了数形结合思想的重要作用．
练习册系列答案
相关题目
如图，正方形ABCD中，AC为对角线，E、F分别是边AB、AD上的两点，且CE=CF．
，∠B＝
，以C为圆心，CA为半径的圆交AB于点D，若AC＝12，求
的长．
的长．