题目内容
2.化简分式:$\frac{3m-12}{{m}^{2}-16}$,若m是不等式组$\left\{\begin{array}{l}{x-2>0}\\{\frac{x+2}{3}+2≥x}\end{array}\right.$的整数解,求此分式的值.分析 先根据分式混合运算的法则把原式进行化简,再求出m的值代入进行计算即可.
解答 解:原式=$\frac{3(m-4)}{(m+4)(m-4)}$
=$\frac{3}{m+4}$,
解不等式组$\left\{\begin{array}{l}x-2>0\\ \frac{x+2}{3}+2≥x\end{array}\right.$得,2<x≤4,
∵m是不等式组的整数解,
∴当x=3时,原式=$\frac{3}{7}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.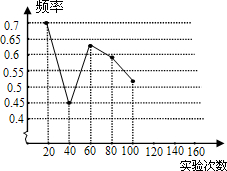 一粒木质中国象棋棋子“車”,它的正面雕刻一个“車”字,它的反面是平的,将棋子从一定高度下抛,落地反弹后可能是“車”字面朝上,也可能是“車”字朝下.由于棋子的两面不均匀,为了估计“車”字朝上的机会,某实验小组做了棋子下抛实验,并把实验数据整理如下:
一粒木质中国象棋棋子“車”,它的正面雕刻一个“車”字,它的反面是平的,将棋子从一定高度下抛,落地反弹后可能是“車”字面朝上,也可能是“車”字朝下.由于棋子的两面不均匀,为了估计“車”字朝上的机会,某实验小组做了棋子下抛实验,并把实验数据整理如下:
(1)请将表中数据补充完整,并画出折线统计图中剩余部分.
(2)如果实验继续进行下去,根据上表数据,这个实验的频率将接近于该事件发生的机会,请估计这个机会约是多少?
(3)在(2)的基础上,进一步估计:将该“車”字棋子,按照实验要求连续抛2次,则刚好使“車”字一次字面朝上,一次朝下的可能性为多少?
 一粒木质中国象棋棋子“車”,它的正面雕刻一个“車”字,它的反面是平的,将棋子从一定高度下抛,落地反弹后可能是“車”字面朝上,也可能是“車”字朝下.由于棋子的两面不均匀,为了估计“車”字朝上的机会,某实验小组做了棋子下抛实验,并把实验数据整理如下:
一粒木质中国象棋棋子“車”,它的正面雕刻一个“車”字,它的反面是平的,将棋子从一定高度下抛,落地反弹后可能是“車”字面朝上,也可能是“車”字朝下.由于棋子的两面不均匀,为了估计“車”字朝上的机会,某实验小组做了棋子下抛实验,并把实验数据整理如下:| 实验次数 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 |
| “車”字朝上的频数 | 14 | 18 | 38 | 47 | 52 | 66 | 78 | 88 |
| 相应的频率 | 0.7 | 0.45 | 0.63 | 0.59 | 0.52 | 0.55 | 0.56 | 0.55 |
(2)如果实验继续进行下去,根据上表数据,这个实验的频率将接近于该事件发生的机会,请估计这个机会约是多少?
(3)在(2)的基础上,进一步估计:将该“車”字棋子,按照实验要求连续抛2次,则刚好使“車”字一次字面朝上,一次朝下的可能性为多少?
11.下列命题中的真命题是( )
| A. | 菱形是中心对称图形,但不是轴对称图形 | |
| B. | 相等的弦所对应的弦心距相等 | |
| C. | 直角三角形的外心和重心之间的距离等于斜边的六分之一 | |
| D. | 三角形的内心是三角形三边的中垂线的交点 |
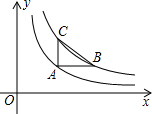 如图,已知点A在反比例函数y=$\frac{2}{x}$的图象上,点B,C分别在反比例函数y=$\frac{4}{x}$的图象上,且AB∥x轴,AC∥y轴,若AB=2AC,则点A的坐标为(2,1).
如图,已知点A在反比例函数y=$\frac{2}{x}$的图象上,点B,C分别在反比例函数y=$\frac{4}{x}$的图象上,且AB∥x轴,AC∥y轴,若AB=2AC,则点A的坐标为(2,1).


