题目内容
8. 如图,已知AB是⊙O的一条弦,点C是⊙O的优弧ACB上的一个动点(不与A,B不重合),
如图,已知AB是⊙O的一条弦,点C是⊙O的优弧ACB上的一个动点(不与A,B不重合),(1)设∠ACB的平分线与劣弧AB交于点P,试猜想点P劣弧AB上的位置是否会随点C的运动而变化?请说明理由
(2)如图②,设AB=8,⊙O的半径为5,在(1)的条件下,四边形ACBP的面积是否为定值?若是定值,请求出这个定值;若不是定值,请求出ACBP的面积的取值范围.
分析 (1)点P位置不会随点C的运动而变化,根据角平分线的定义得到∠ACP=∠BCP,于是得到$\widehat{AP}$=$\widehat{BD}$,即P是劣弧AB的中点.即可得到点P位置不会变化.
(2)如图,连接OP,交AB于E,根据垂径定理得到OP⊥AB,AE=$\frac{1}{2}$AB=4.根据勾股定理得到OE=$\sqrt{{5}^{2}-{4}^{2}}$=3,PE=2.求得S△ABP=$\frac{1}{2}×8×2$.于是得到当CP经过圆心O时,如图,C到AB距离最大,即△ABC的AB边上的最大高线是CE=8.求得四边形ACBP的最大面积是40.即可得到结论.
解答  解:(1)点P位置不会随点C的运动而变化,
解:(1)点P位置不会随点C的运动而变化,
理由:如图1,
∵CP平分∠ACB,
∴∠ACP=∠BCP,
∴$\widehat{AP}$=$\widehat{BD}$,
即P是劣弧AB的中点.
∴点P位置不会变化.
(2)∵△ABC的面积不是定值,△ABP的面积为定值
∴四边形ACBP的面积不是定值.
如图,连接OP,交AB于E,
∵$\widehat{AP}$=$\widehat{PB}$,OP是半径.
∴OP⊥AB,AE=$\frac{1}{2}$AB=4.
∵OA=5.
∴OE=$\sqrt{{5}^{2}-{4}^{2}}$=3,PE=2.
∴S△ABP=$\frac{1}{2}×8×2$.
∴当CP经过圆心O时,如图,C到AB距离最大,即△ABC的AB边上的最大高线是CE=8.
∵AB=8,
∴△ABC的最大面积是32.
∴四边形ACBP的最大面积是40.
综上,四边形ACBP的面积不是定值,它的取值范围是8<S四边形ACBP≤40.
点评 本题考查了圆周角定理,三角形的面积的计算,勾股定理,熟练掌握圆周角定理是解题的关键.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案| A. | 2 | B. | 3 | C. | 4 | D. | $\sqrt{2}$ |
| A. | 有两个角是60°的三角形 | B. | 有一个角是60°的等腰三角形 | ||
| C. | 有两个外角相等的等腰三角形 | D. | 三边都相等的三角形 |
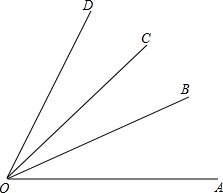 如图,OB、OC把∠AOD平分成三个相等的角,则OB是∠AOC的平分线,OC是∠BOD平分线.若OM是∠BOC的平分线,则OM也是∠AOD的平分线.
如图,OB、OC把∠AOD平分成三个相等的角,则OB是∠AOC的平分线,OC是∠BOD平分线.若OM是∠BOC的平分线,则OM也是∠AOD的平分线. 如图,线段AB表示一根对折以后的绳子,现从P处把其中一条绳子剪断,剪断后的各段绳子中最长的一段为35cm,若AP=$\frac{1}{3}$PB,则这条绳子的原长为93$\frac{1}{3}$cm.
如图,线段AB表示一根对折以后的绳子,现从P处把其中一条绳子剪断,剪断后的各段绳子中最长的一段为35cm,若AP=$\frac{1}{3}$PB,则这条绳子的原长为93$\frac{1}{3}$cm.