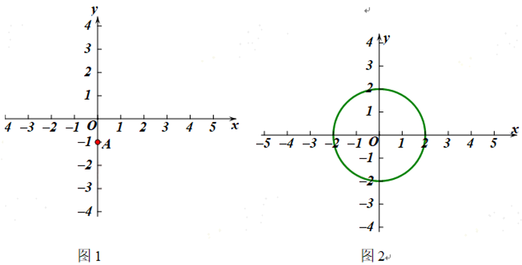
题目内容
【题目】对于平面内
和外一点
，若过点的直线
与有两个不同的公共点
，点
为直线上的另一点，且满足
(如图1所示)，则称点是点关于的密切点．
已知在平面直角坐标系
中， 
的半径为2，点
．
(1)在点
中，是点关于的密切点的为__________．
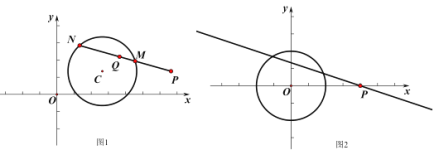
(2)设直线方程为
，如图2所示，
①
时，求出点关于的密切点的坐标；
②
的圆心为
，半径为2，若上存在点关于的密切点，直接写出
的取值范围．
【答案】（1）E；（2）①
；②
或
【解析】
(1)用假设法通过特殊位置判断;
（2）①拿出直线解析式，联立与圆的位置根据勾股定理求得M,N两点的横坐标，根据题目条件信息转化即可求解.
②作出点
关于
的密切点的运动轨迹，根据图像即可求出取值范围.
解：(1)当圆心在坐标原点上时，直线为
时，易得：
,
,
∵
，设Q点坐标为
,
解得
，
故
是点关于
的密切点.
(2)①依题意直线
方程
过定点
∴直线方程为
如右图，作
轴于点
，
轴于点
．
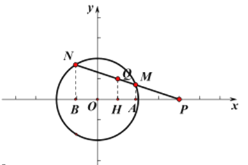
设
由
得
∴
点的横坐标
是方程的两根
解得
∴
，
，
∴
∴
∴
∴
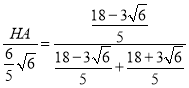
②点关于的密切点的轨迹为线段,为切点弦
(不含端点)．
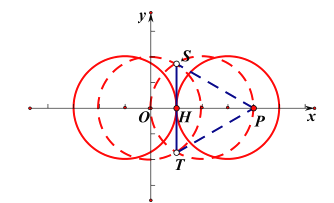
或
练习册系列答案
相关题目
