题目内容
【题目】在平面直角坐标系xOy中,若点P和点![]() 关于x轴对称,点
关于x轴对称,点![]() 和点
和点![]() 关于直线l对称,则称点
关于直线l对称,则称点![]() 是点P关于x轴,直线l的二次对称点.
是点P关于x轴,直线l的二次对称点.
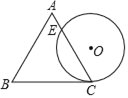
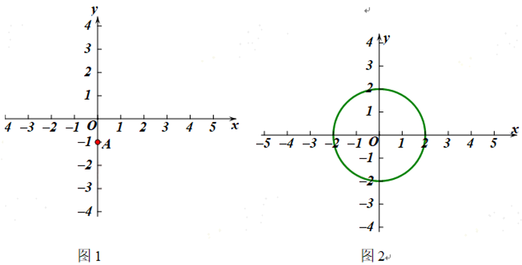
(1)如图1,点A(0,-1).
①若点B是点A关于x轴,直线![]() :x=2的二次对称点,则点B的坐标为 ;
:x=2的二次对称点,则点B的坐标为 ;
②点C (-4,1)是点A关于x轴,直线![]() :x=a的二次对称点,则a的值为 ;
:x=a的二次对称点,则a的值为 ;
③点D(-1,0)是点A关于x轴,直线![]() 的二次对称点,则直线
的二次对称点,则直线![]() 的表达式为 ;
的表达式为 ;
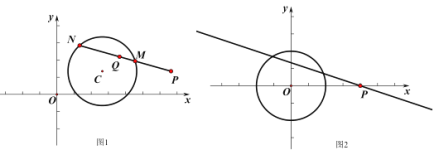
(2)如图2,O的半径为2.若O上存在点M,使得点M′是点M关于x轴,直线![]() :x = b的二次对称点,且点M′在射线
:x = b的二次对称点,且点M′在射线![]() (x≥0)上,b的取值范围是 ;
(x≥0)上,b的取值范围是 ;
(3)E(0,t)是y轴上的动点,E的半径为2,若E上存在点N,使得点N′是点N关于x轴,直线![]() :
:![]() 的二次对称点,且点N′在x轴上,求t的取值范围.
的二次对称点,且点N′在x轴上,求t的取值范围.
【答案】(1)①(4,1),②-2,③y =- x;(2)b的取值范围是-1≤b≤![]() ;(3)-4≤t≤4
;(3)-4≤t≤4
【解析】
(1)①根据题目中二次对称点的定义,可以求得点B的坐标;
②根据题目中二次对称点的定义,可以求得a的值;
③根据题目中二次对称点的定义,可以求得直线l3的表达式;
(2)根据题意可以画出相应的图形,利用分类讨论的方法即可解答本题;
(3)根据题意和对称的二次对称点的定义,根据题目中的图形,可以求得t的取值范围,本题得以解决.
解:(1)① 点B的坐标为 (4,1)
② a的值为-2
③直线l3的表达式为y =- x
(2)如图2,
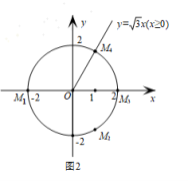
设O与x轴的两个交点为![]() (-2,0),
(-2,0),![]() (2,0),
(2,0),
与射线![]() (x≥0)的交点为
(x≥0)的交点为![]() ,则
,则![]() 的坐标为(1,
的坐标为(1,![]() ).
).
![]() 关于x轴的对称点为
关于x轴的对称点为![]() .
.
当点M在![]() 的位置时,b=-1,
的位置时,b=-1,
当点M在![]() 的位置时,b=1,
的位置时,b=1,
当点M在![]() 的位置时,b=1,
的位置时,b=1,
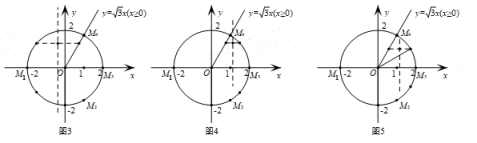
当点M在劣弧![]() 上时(如图3),-1≤b≤1,
上时(如图3),-1≤b≤1,
当点M在劣弧![]() 上时(如图4),b的值比1大,当到劣弧
上时(如图4),b的值比1大,当到劣弧![]() 的中点时,达到最大值(如图5),最大值为
的中点时,达到最大值(如图5),最大值为![]() .综上,b的取值范围是-1≤b≤
.综上,b的取值范围是-1≤b≤![]() .
.
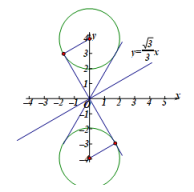
(3)∵x轴和直线![]() 关于直线
关于直线![]() 对称,
对称,
直线![]() 和直线
和直线![]() 关于x轴对称,
关于x轴对称,
∴E只要与直线![]() 和
和![]() 有交点即可.
有交点即可.
∴t 的取值范围是:-4≤t≤4
. 

 阅读快车系列答案
阅读快车系列答案【题目】二次函数![]() 上部分点的横坐标x与纵坐标y的对应值如下表:
上部分点的横坐标x与纵坐标y的对应值如下表:
x | … |
|
| 0 | 1 | 2 | 3 | … |
y | … | 3 |
| 0 |
| 0 | m | … |

(1)直接写出此二次函数的对称轴 ;
(2)求b的值;
(3)直接写出表中的m值,m= ;
(4)在平面直角坐标系xOy中,画出此二次函数的图象.
【题目】每年4月23日是世界读书日,某校为了解学生课外阅读情况,随机抽取20名学生,对每人每周用于课外阅读的平均时间(单位:min)进行调查,过程如下:
收集数据:
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
整理数据:
课外阅读平均时间x(min) | 0≤x<40 | 40≤x<80 | 80≤x<120 | 120≤x<160 |
等级 | D | C | B | A |
人数 | 3 | a | 8 | b |
分析数据:
平均数 | 中位数 | 众数 |
80 | m | n |
请根据以上提供的信息,解答下列问题:
(1)填空:a= ,b= ;m= ,n= ;
(2)已知该校学生500人,若每人每周用于课外阅读的平均时间不少于80min为达标,请估计达标的学生数;
(3)设阅读一本课外书的平均时间为260min,请选择适当的统计量,估计该校学生每人一年(按52周计)平均阅读多少本课外书?