题目内容

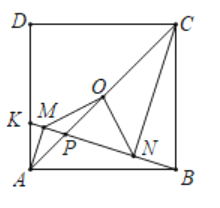
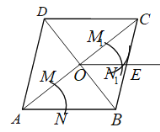
【题目】如图，菱形的对角线相交于点按下列步骤作图：①以点为圆心，任意长为半径作弧，分别交于点；②以点为圆心，长为半径作弧，交于点；③点为圆心，以长为半径作弧，在内部交②中所作的圆弧于点；④过点作射线交于点．，四边形的面积为（ ）

A.B.C.D.

【答案】C

【解析】

利用作法得到∠COE=∠OAB，则OE∥AB，利用菱形的性质可得OE∥CD，然后运用相似三角形的性质进行计算．

解：∵四边形ABCD为菱形，

∴S菱形ABCD=8=24，S△BCD=12.

由作法得∠COE=∠OAB，
∴OE∥AB，
∵四边形ABCD为菱形，
∴OD=OB，CD∥AB,

∴OE∥CD，

∴=（）2=.

∴S△OBE=3.

∴S四边形DOEC=12-3=9.

故选C.

练习册系列答案
相关题目

【题目】在学习《用频率估计概率》这一节课后，数学兴趣小组设计了摸球试验：在一个不透明的盒子里装有质地大小都相同的红球和黑球共个，将球搅匀后从中随机摸出一个记下颜色，放回，再重复进行下一次试验，下表是他们整理得到的试验数据：

摸球的次数

摸到红球的次数

摸到红球的频率

（1）试估计：盒子中有红球 个；

（2）若从盒子中一次性摸出两个球，用画树状图或列表的方法求出一次性摸出的两个球都是红球的概率．

【题目】在平面直角坐标系xOy中，点A（t，0），B（t+2，0），C（n，1），若射线OC上存在点P，使得△ABP是以AB为腰的等腰三角形，就称点P为线段AB关于射线OC的等腰点．

（1）如图，t＝0，

①若n＝0，则线段AB关于射线OC的等腰点的坐标是　 　；

②若n＜0，且线段AB关于射线OC的等腰点的纵坐标小于1，求n的取值范围；

（2）若n＝，且射线OC上只存在一个线段AB关于射线OC的等腰点，则t的取值范围是　 　．

【题目】（1）如图，已知线段和点O，利用直尺和圆规作，使点O是的内心（不写作法，保留作图痕迹）；

（2）在所画的中，若，则的内切圆半径是______．

【题目】如图，AB是⊙O的直径，C为⊙O上一点，AD和过点C的切线互相垂直，垂足为D．

（1）求证：；

（2）若，，求CD的长．

【题目】如图，在中，于点，动点从点出发以每秒个单位长度的速度向终点运动，当点与点不重合时，过点作交边于点，以为边作使点在点的下方，且，设与重叠部分图形的面积为，点的运动时间为秒．

（1）的长为 ；

（2）当点落在边上时，求的值；

（3）当与重叠部分图形为四边形时，求与之间的函数关系式；

（4）若射线与边交于点连结，当的垂直平分线经过的顶点时，直接写出的值．

【题目】如图，边长为1的正方形ABCD中，点K在AD上，连接BK，过点A，C作BK的垂线，垂足分别为M，N，点O是正方形ABCD的中心，连接OM，ON．

（1）求证：AM=BN；

（2）请判断△OMN的形状，并说明理由；

（3）若点K在线段AD上运动（不包括端点），设AK=x，△OMN的面积为y，求y关于x的函数关系式（写出x的范围）；若点K在射线AD上运动，且△OMN的面积为，请直接写出AK长．

【题目】某中学开展“阳光体育一小时”活动，按学校实际情况，决定开设A：踢毽子；B：篮球；C：跳绳；D：乒乓球四种运动项目．为了解学生最喜欢哪一种运动项目，随机抽取了一部分学生进行调查，并将调查结果绘制成如下两个统计图．请结合图中的信息解答下列问题：

（1）本次共调查了________名学生；

（2）在扇形统计图中，“B”所在扇形的圆心角是________度；

（3）将条形统计图补充完整；

（4）若该中学有1200名学生，喜欢篮球运动的学生约有________名．

【题目】已知，在平面直角坐标系中，点为坐标原点，直线与轴的正半轴交于点A，与轴的负半轴交于点B， ，过点A作轴的垂线与过点O的直线相交于点C，直线OC的解析式为，过点C作轴，垂足为．

（1）如图1，求直线的解析式；

（2）如图2，点N在线段上，连接ON，点P在线段ON上，过P点作轴，垂足为D，交OC于点E，若，求的值；

（3）如图3，在（2）的条件下，点F为线段AB上一点，连接OF，过点F作OF的垂线交线段AC于点Q，连接BQ，过点F作轴的平行线交BQ于点G，连接PF交轴于点H，连接EH，若，求点P的坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网