Question

【题目】已知∠BOC＝60°，OF平分∠BOC.若AO⊥BO，OE平分∠AOC，则∠EOF的度数是(　　)

A. 45°

B. 15°

C. 30°或60°

D. 45°或15°

Answer 1

【答案】A

【解析】

根据垂线的定义，可得∠AOB的度数，根据角的和差，可得∠AOC的度数，根据角平分线的性质，可得∠COE、∠COF的度数，根据角的和差，可得答案．

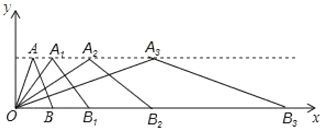
如图1，

由AO⊥BO，得∠AOB＝90°，

由角的和差，得∠AOC＝∠AOB＋∠BOC＝150°，

∵OE平分∠AOC，OF平分∠BOC，

∴∠COE＝∠AOC＝×150°＝75°，∠COF＝∠BOC＝×60°＝30°，

由角的和差，得∠EOF＝∠COE－∠COF＝75°－30°＝45°；

如图2，

由AO⊥BO，得∠AOB＝90°，

由角的和差，得∠AOC＝∠AOB－∠BOC＝30°，

∵OE平分∠AOC，OF平分∠BOC，

∴∠COE＝∠AOC＝×30°＝15°，∠COF＝∠BOC＝×60°＝30°，

由角的和差，得∠EOF＝∠COE＋∠COF＝15°＋30°＝45°，

故选A.