题目内容
△ABC中,∠ACB=90°,AC=BC,M是AB边的中点.
(1)如图1,若P,Q分别在边BC和CA上,且BP=CQ.通过观察或测量,猜想△MPQ的形状,并给予证明;
(2)如图2,若P,Q分别在BC和CA的延长线上,且BP=CQ,△MPQ的形状与(1)中相比,是否会有变化?请说明理由.

(1)如图1,若P,Q分别在边BC和CA上,且BP=CQ.通过观察或测量,猜想△MPQ的形状,并给予证明;
(2)如图2,若P,Q分别在BC和CA的延长线上,且BP=CQ,△MPQ的形状与(1)中相比,是否会有变化?请说明理由.

考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:(1)连接CM,易证△CMQ≌△BMP,可得∠BMP=∠CMQ,QM=PM,根据∠CMP+∠BMP=90°即可求得△MPQ是等腰直角三角形,即可解题;
(2)连接CM,易证△AQM≌△CPM,可得QM=PM,∠QMA=∠PMC,根据∠PMC+∠PMA=90°即可求得△MPQ是等腰直角三角形,即可解题.
(2)连接CM,易证△AQM≌△CPM,可得QM=PM,∠QMA=∠PMC,根据∠PMC+∠PMA=90°即可求得△MPQ是等腰直角三角形,即可解题.
解答:证明:

(1)连接CM,
∵∠ACB=90°,AC=BC,M是AB边的中点,
∴CM=BM,∠ACM=∠B=45°,CM⊥AB,
∵在△CMQ和△BMP中,
,
∴△CMQ≌△BMP,(SAS)
∴∠BMP=∠CMQ,QM=PM,
∵∠CMP+∠BMP=90°,
∴∠CMQ+∠CMP=90°,即∠QMP=90°;
∴△MPQ是等腰直角三角形;
(2)连接CM,
∵∠ACB=90°,AC=BC,M是AB边的中点,
∴CM=AM,∠ACM=∠CAM=45°,CM⊥AB,
∴∠PCM=45°+90°=135°,
∠QAM=180°-45°=135°,
∵在△AQM和△CPM中,
,
∴△AQM≌△CPM,(SAS)
∴QM=PM,∠QMA=∠PMC,
∵∠PMC+∠PMA=90°,
∴∠QMA+∠PMA=90°,
∴△MPQ是等腰直角三角形.

(1)连接CM,
∵∠ACB=90°,AC=BC,M是AB边的中点,
∴CM=BM,∠ACM=∠B=45°,CM⊥AB,
∵在△CMQ和△BMP中,
|
∴△CMQ≌△BMP,(SAS)
∴∠BMP=∠CMQ,QM=PM,
∵∠CMP+∠BMP=90°,
∴∠CMQ+∠CMP=90°,即∠QMP=90°;
∴△MPQ是等腰直角三角形;
(2)连接CM,
∵∠ACB=90°,AC=BC,M是AB边的中点,
∴CM=AM,∠ACM=∠CAM=45°,CM⊥AB,
∴∠PCM=45°+90°=135°,
∠QAM=180°-45°=135°,
∵在△AQM和△CPM中,
|
∴△AQM≌△CPM,(SAS)
∴QM=PM,∠QMA=∠PMC,
∵∠PMC+∠PMA=90°,
∴∠QMA+∠PMA=90°,
∴△MPQ是等腰直角三角形.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△CMQ≌△BMP和△AQM≌△CPM是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知,如图,AB=AC,BD平分∠ABC,CD平分∠ACB.求证:AD⊥BC.
已知,如图,AB=AC,BD平分∠ABC,CD平分∠ACB.求证:AD⊥BC.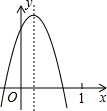 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论: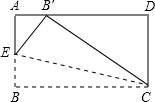 如图,一块矩形纸片的宽CD为2cm,点E在AB上,如果沿图中的EC对折,B点刚好落在AD上,此时∠BCE=15°,则BC的长为
如图,一块矩形纸片的宽CD为2cm,点E在AB上,如果沿图中的EC对折,B点刚好落在AD上,此时∠BCE=15°,则BC的长为