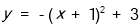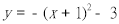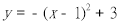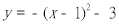Question

如图，已知AD∥BC，∠PAB的平分线与∠CBA的平分线相交于E，CE的连线交AP于D．

求证：AD+BC=AB．

Answer 1

证明见解析.

【解析】

试题分析：首先在AB上截取AF=AD，由AE平分∠PAB，利用SAS即可证得△DAE≌△FAE，继而可证得∠EFB=∠C，然后利用AAS证得△BEF≌△BEC，即可得BC=BF，继而证得AD+BC=AB．

试题解析：证明：在AB上截取AF=AD，

∵AE平分∠PAB，

∴∠DAE=∠FAE，

在△DAE和△FAE中，

∵，

∴△DAE≌△FAE（SAS），

∴∠AFE=∠ADE，

∵AD∥BC，

∴∠ADE+∠C=180°，

∵∠AFE+∠EFB=180°，

∴∠EFB=∠C，

∵BE平分∠ABC，

∴∠EBF=∠EBC，

在△BEF和△BEC中，

∵，

∴△BEF≌△BEC（AAS），

∴BC=BF，

∴AD+BC=AF+BF=AB．

考点：全等三角形的判定与性质．