题目内容
如图①,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.
(1)求证:△BCP≌△DCP;
(2)求证:∠DPE=∠ABC;
(3)把正方形ABCD改为菱形,其它条件不变(如图②),若∠ABC=58°,则∠DPE= 度.

解:(1)证明:在正方形ABCD中,BC=DC,∠BCP=∠DCP=45°,
∵在△BCP和△DCP中, ,
,
∴△BCP≌△DCP(SAS)。 4分
(2)证明:由(1)知,△BCP≌△DCP,
∴∠CBP=∠CDP。
 ∵PE=PB,∴∠CBP=∠E。∴∠DPE=∠DCE。
∵PE=PB,∴∠CBP=∠E。∴∠DPE=∠DCE。
∵∠1=∠2(对顶角相等),
∴180°﹣∠1﹣∠CDP=180°﹣∠2﹣∠E,
即∠DPE= ∠DCE。
∠DCE。
∵AB∥CD,
∴∠DCE=∠ABC。
∴∠DPE=∠ABC。
(3)58°

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目



 上的一点,过点M作x轴、y轴的垂线,分别交直线
上的一点,过点M作x轴、y轴的垂线,分别交直线 于点D、C两点,若直线
于点D、C两点,若直线 交于点A,与x轴相交于点B,则AD•BC的值为( )
交于点A,与x轴相交于点B,则AD•BC的值为( ) B.
B. C.
C. D.
D.

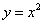 。如图(1),平移抛物线C1得到抛物线C2,C2经过C1的顶点O和A(2,0),C2的对称轴分别交C1、C2于点B、D。
。如图(1),平移抛物线C1得到抛物线C2,C2经过C1的顶点O和A(2,0),C2的对称轴分别交C1、C2于点B、D。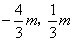 )在直线MG上。问:当m为何值时,在抛物线C3上存在点Q,使得以M、N、P、Q为顶点的四边形为平行四边形?
)在直线MG上。问:当m为何值时,在抛物线C3上存在点Q,使得以M、N、P、Q为顶点的四边形为平行四边形?