题目内容
已知:抛物线C1: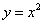 。如图(1),平移抛物线C1得到抛物线C2,C2经过C1的顶点O和A(2,0),C2的对称轴分别交C1、C2于点B、D。
。如图(1),平移抛物线C1得到抛物线C2,C2经过C1的顶点O和A(2,0),C2的对称轴分别交C1、C2于点B、D。
(1)求抛物线C2的解析式;
(2)探究四边形ODAB的形状并证明你的结论;
(3)如图(2),将抛物线C2向m个单位下平移(m>0)得抛物线C3,C3的顶点为G,与y轴交于M。点N是M关于x轴的对称点,点P(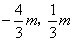 )在直线MG上。问:当m为何值时,在抛物线C3上存在点Q,使得以M、N、P、Q为顶点的四边形为平行四边形?
)在直线MG上。问:当m为何值时,在抛物线C3上存在点Q,使得以M、N、P、Q为顶点的四边形为平行四边形?
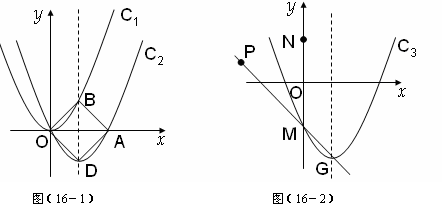

解:(1)设抛物线C2的解析式为 ,把A(2,0)代入得,
,把A(2,0)代入得, 。
。
 ∴抛物线C2的解析式为
∴抛物线C2的解析式为 。
。
(2)四边形ODAB是正方形,理由如下:
设BD与x轴交于点E,
∵ ,
,
∴D(1,-1),B(1,1),E(1,0)。
 ∴OE=EA=ED=EB=1,且OA⊥BD,
∴OE=EA=ED=EB=1,且OA⊥BD,
∴ODAB为正方形。
(3)设抛物线C3的解析式为 。
。
则M(0, ),N(0,
),N(0, ),
),
 ,∴G(1,
,∴G(1, )。
)。
设直线MG为 ,则
,则 ,
,
解得 ,
,
∴直线MG为 。
。
如图,若P、M、N、R四点构成平行四边形,
只能有三种情况,而显然R在第三象限不可能,
∴R只可能在四象限或二象限。
① 若R在第四象限,∵M、N关于点O对称,
所以P、R也关于点O对称,
∴R( ),
),
过N作NQ∥PM,
∴直线NQ为 ,
,
当 时,
时, ,
,
∴R在直线NR上。
把R( )代入
)代入 ,得
,得

∵ ,∴
,∴ 。
。
② 若R在第二象限,则PR∥MN,PM∥NR,,且R在NQ上
若R在第二象限,则PR∥MN,PM∥NR,,且R在NQ上
∵MN⊥x轴,∴PR⊥x轴,则R( )
)
∵R在NQ上,
∴ ,
,
又∵R在抛物线C3上,则
∵ ,∴
,∴ 。
。
∴当 或
或 时,在抛物线C3上存在点Q,使得以M、N、P、Q为顶点的
时,在抛物线C3上存在点Q,使得以M、N、P、Q为顶点的
四边形为平行四边形。

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 是方程mx+3y=1的一个解,则m的值是 .
是方程mx+3y=1的一个解,则m的值是 .






 .1060
.1060  C.960 D.1040
C.960 D.1040 °
°