题目内容
如图，将图①所示的正三角形连接扣边中点进行分割，得到图②；再将图②中最中间的小正三角形按同样的方式进行分割，得到图③；再将图③中最中间的小正三角形按同样的方式进行分割…，则得到的第六个图中，共有
21
21
个正三角形．分析：观察图形：图①中有1个正三角形；图②中有1+4=1+4×1=5个正三角形；图③中有1+4+4=1+4×2=9个正三角形…依此类推图⑤中有1+4×4=17个正三角形，图⑥中正三角形的个数为1+4×5=21．
解答：解：∵由图①得：三角形的个数为1，
由图②得：三角形的个数为1+4×1=5，
由图③得：三角形的个数为1+4×2=9，
…
∴第六个图中，三角形的个数为1+4×5=21．
故答案为21．
由图②得：三角形的个数为1+4×1=5，
由图③得：三角形的个数为1+4×2=9，
…
∴第六个图中，三角形的个数为1+4×5=21．
故答案为21．
点评：本题主要考查图形的变化，总结归纳规律，关键在于逐个观察分析图形，正确分析正三角形个数的变化规律．
练习册系列答案
备战中考寒假系列答案
相关题目
如图（1），将正方体左上部切去一个小三棱柱（图中M、N都是正方体的棱的中点），得到如图（2）所示的几何体，从正面、上面、左面看（2）中的几何体，看到的图形面积分别为S正、S上、S左，则（ ）| A、S正=S上=S左 | B、S正＜S上=S左 | C、S上＜S左＜S正 | D、S上＜S左=S正 |
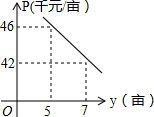为响应薄熙来书记建设“森林重庆”的号召，某园艺公司从2010年9月开始积极进行植树造林．该公司第x月种植树木的亩数y（亩）与x之间满足y=x+4，（其中x从9月算起，即9月时x=1，10月时x=2，…，且1≤x≤6，x为正整数）．由于植树规模扩大，每亩的收益P（千元）与种植树木亩数y（亩）之间存在如图（25题图）所示的变化趋势．
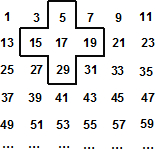将连续的奇数1，3，5，7，…，排成如下图的数表，用图中所示的十字框可任意框出5个数．
的长度；
