��Ŀ����
��ͼ��1������ƽ��ֱ������ϵ�У�����ABCO��B������Ϊ��4��3����������y=- x2+bx+c��������ABCO�Ķ���B��C��DΪBC���е㣬ֱ��AD��y�ύ��E�㣬��F��ֱ��AD���Һ�����Ϊ6��
x2+bx+c��������ABCO�Ķ���B��C��DΪBC���е㣬ֱ��AD��y�ύ��E�㣬��F��ֱ��AD���Һ�����Ϊ6��

��1����������߽���ʽ���ж�F���Ƿ��ڸ��������ϣ�
��2����ͼ������P�ӵ�C���������߶�CB��ÿ��1����λ���ȵ��ٶ����յ�B�˶���
ͬʱ������M�ӵ�A���������߶�AE��ÿ�� ����λ���ȵ��ٶ����յ�E�˶�������P��PH��OA������ΪH������MP��MH�����P���˶�ʱ��Ϊt�룮
����λ���ȵ��ٶ����յ�E�˶�������P��PH��OA������ΪH������MP��MH�����P���˶�ʱ��Ϊt�룮
����EP+PH+HF�Ƿ�����Сֵ������У����t��ֵ�����û�У���˵�����ɣ�
������PMH�ǵ��������Σ������ʱt��ֵ��
 �⣺��1���߾���ABCO��B������Ϊ��4��3����������y=-
�⣺��1���߾���ABCO��B������Ϊ��4��3����������y=- x2+bx+c��������ABCO�Ķ���B��C��DΪBC���е㣬
x2+bx+c��������ABCO�Ķ���B��C��DΪBC���е㣬��C������Ϊ����0��3����A������Ϊ����4��0����D������Ϊ����2��3����
��B��C�����y=-
 x2+bx+c�ã�
x2+bx+c�ã� ��
����ã�
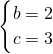 ��
����������߽���ʽΪ��y=-
 x2+2x+3��
x2+2x+3�����D��A��ֱ�߽���ʽΪ��y=ax+k��
��
 ��
����ã�
 ��
����ֱ��AD�Ľ���ʽΪ��y=-
 x+6��
x+6��
�ߵ�F��ֱ��AD���Һ�����Ϊ6��
��y=-
 ��6+6=-3��
��6+6=-3����F������Ϊ����6��-3������F����������߽���ʽ�ó����ұ�=-
 ��36+12+3=-3��
��36+12+3=-3����F���ڸ��������ϣ�
��2���١�E��0��6����
��CE=CO��
��ͼ1��
����CF��x����H�䣬��H����x��Ĵ��߽�BC��P�䣬
��P �˶���P�䣬��H�˶���H��ʱ��EP+PH+HF��ֵ��С��
��ֱ��CF�Ľ���ʽΪy=ax+b
��C��0��3����F��6��-3��

��
 ��
����
 ��
����y=-x+3��
��y=0ʱ��x=3��
��H�䣨3��0��
��CP=3��
��t=3��
����ͼ2����M��MN��OA��OA��N��
��NM��EO��
���AMN�ס�AEO��
��
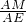 =
= =
= ��
����EO=6��AO=4��

��AE=2
 ��
����
 =
= =
=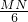 ��
����AN=t��MN=
 t
tI����ͼ2����PM=HMʱ��M��PH�Ĵ�ֱƽ�����ϣ�
��MN=
 PH��
PH����MN=
 t=
t= ��
�����ã�t=1
II����ͼ3����PH=HMʱ��MH=3��MN=
 t��
t��HN=OA-AN-OH=4-2t��

��Rt��HMN��
MN2+HN2=MH2��
��
 t��2+��4-2t��2=32��
t��2+��4-2t��2=32�������ã�25t2-64t+28=0
��ã�t1=2����ȥ����t2=
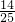 ��
��III����ͼ4����ͼ5����PH=PMʱ��PM=3��MT=|3-
 t|��
t|��PT=BC-CP-BT=|4-2t|��
��Rt��PMT��MT2+PT2=PM2��
��3-
 t��2+��4-2t��2=32��
t��2+��4-2t��2=32��������25t2-100t+64=0��
��ã�t1=
 ��t2=
��t2= ��
��������������t=
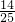 ��
�� ��1��
��1�� ��
����������1�����ݾ��ε����ʵó�A��C��D�����꣬�����ó������߽���ʽ�������AD�Ľ���ʽ��������ͼ���ϵ�����ʵó����ɣ�
��2�������ȵó�P��λ�ã������FC�Ľ���ʽ�����ɵó�t��ֵ��
�ڷֱ���ݵ�PM=HMʱ����PH=HMʱ����PH=PMʱ������ɣ�
������������Ҫ�����˶��κ������ۺ�Ӧ���Լ����ɶ�����Ӧ�ú����������ε��ж������ʵ�֪ʶ�����ݷ������۵�˼��ó�ע�ⲻҪ©���ǽ���ؼ���

��ϰ��ϵ�д�
 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�
�����Ŀ
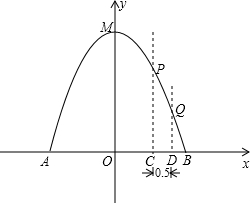 �������Բ����Ͱ�ĺ�Ⱥ��Բ��ƣ�����M��Ϊ���㣬�����߶Գ���Ϊy�ᣬˮƽ����Ϊx�Ὠ��ƽ��ֱ������ϵ��
�������Բ����Ͱ�ĺ�Ⱥ��Բ��ƣ�����M��Ϊ���㣬�����߶Գ���Ϊy�ᣬˮƽ����Ϊx�Ὠ��ƽ��ֱ������ϵ�� ˮ����������ĵ�ˮƽ����Ϊ1m���ﵽ��ߣ��߶�Ϊ3m��
ˮ����������ĵ�ˮƽ����Ϊ1m���ﵽ��ߣ��߶�Ϊ3m��




