题目内容
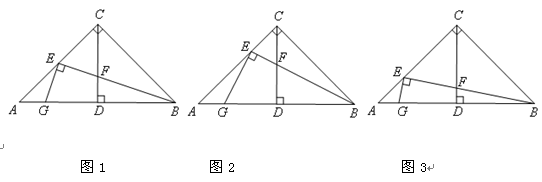
在Rt△ABC中,∠ACB=90 ,AC=BC,CD⊥AB于点D,点E为AC边上一点,联结BE交CD于点F,过点E作EG⊥BE交AB于点G,
,AC=BC,CD⊥AB于点D,点E为AC边上一点,联结BE交CD于点F,过点E作EG⊥BE交AB于点G,
小题1:如图1,当点E为AC中点时,线段EF与EG的数量关系是 ;
小题2:如图2,当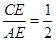 ,探究线段EF与EG的数量关系并且证明;
,探究线段EF与EG的数量关系并且证明;
小题3:如图3,当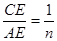 ,线段EF与EG的数量关系是 .
,线段EF与EG的数量关系是 .
 ,AC=BC,CD⊥AB于点D,点E为AC边上一点,联结BE交CD于点F,过点E作EG⊥BE交AB于点G,
,AC=BC,CD⊥AB于点D,点E为AC边上一点,联结BE交CD于点F,过点E作EG⊥BE交AB于点G,小题1:如图1,当点E为AC中点时,线段EF与EG的数量关系是 ;
小题2:如图2,当
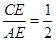 ,探究线段EF与EG的数量关系并且证明;
,探究线段EF与EG的数量关系并且证明;小题3:如图3,当
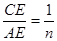 ,线段EF与EG的数量关系是 .
,线段EF与EG的数量关系是 .
小题1:(1) EF=EG
小题2:(2)
 ; ------2分
; ------2分证明:
 过点E作EM⊥CD于点M,作EN⊥AB于点N, ------3分
过点E作EM⊥CD于点M,作EN⊥AB于点N, ------3分∴∠ENA=∠CME=∠EMF=90
 .
.∵CD⊥AB于点D,∴∠CDA=90°. ∴EM∥AD.∠A=∠CEM.
∴△EMC ∽△ANE. ∴
 . ------4分
. ------4分∵EM∥AD,∴∠NEM=90
 .即∠2+∠3=90°.
.即∠2+∠3=90°.∵ EG⊥BE,∴∠3+∠2=90
 ,∴∠1=∠2.
,∴∠1=∠2.∴△EFM ∽△EGN.∴
 . ------5分
. ------5分∵∠ACB=90
 ,AC=BC,∴∠A=45
,AC=BC,∴∠A=45 , ∴tan∠A=
, ∴tan∠A= ="1, " ∴AN=EN.
="1, " ∴AN=EN. ∴
 , ∵
, ∵ , ∴
, ∴ .
.小题3:(3)
 .
.略

练习册系列答案
相关题目
 和
和 是绕点
是绕点 旋转的两个相似三角形,其中
旋转的两个相似三角形,其中 与
与 、
、 与
与 为对应角.
为对应角.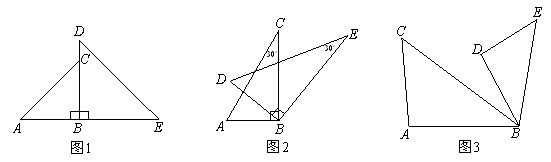
 、
、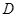 在同一条直线上的位置时,请直接写出线段
在同一条直线上的位置时,请直接写出线段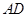 与线段
与线段 的关系;
的关系; 角的直角三角形,且两个三角形旋转到如图2的位置时,试确定线段
角的直角三角形,且两个三角形旋转到如图2的位置时,试确定线段 =
= ,
,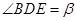 ,在绕点
,在绕点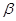 的式子表示夹角的度数;若改变,请说明理由.
的式子表示夹角的度数;若改变,请说明理由.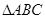 中,
中,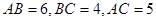 ,点
,点 在边
在边 上,
上,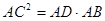 ,那么
,那么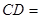 ▲
▲ 
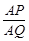 的值等于 ▲
的值等于 ▲ 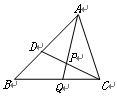
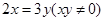 ,则下列比例式成立的是
,则下列比例式成立的是 
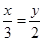
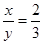

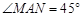 ,连结MC,NC,MN.
,连结MC,NC,MN.
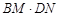 = ;(用含a的代数式表示)
= ;(用含a的代数式表示)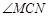 的度数;
的度数;
 =
= ;③AC?BE=12;④3BF=4AC.其中结论正确的个数有( )
;③AC?BE=12;④3BF=4AC.其中结论正确的个数有( )

 =BF.
=BF.