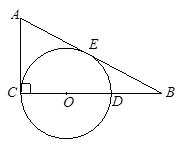
题目内容
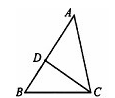
如图,已知在△ABC中,AB=3,AC=2,D是边AB上的一 点,∠ACD=∠B,∠BAC的平分线AQ与CD、BC分别相交于点P和点Q,那么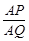 的值等于 ▲
的值等于 ▲ 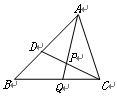
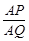 的值等于 ▲
的值等于 ▲ 

根据角平分线的定义得∠BAQ=∠CAP,而∠ACD=∠B,根据相似三角形的判定得到△ABQ∽△ACP,由相似三角形的性质得到 ,把AB=3,AC=2代入即可得到答案.
,把AB=3,AC=2代入即可得到答案.
解:∵AQ平分∠BAC,
∴∠BAQ=∠CAP,
而∠ACD=∠B,
∴△ABQ∽△ACP,
∴ ,
,
又∵AB=3,AC=2,
∴ =
= .
.
故答案为 .
.
 ,把AB=3,AC=2代入即可得到答案.
,把AB=3,AC=2代入即可得到答案.解:∵AQ平分∠BAC,
∴∠BAQ=∠CAP,
而∠ACD=∠B,
∴△ABQ∽△ACP,
∴
 ,
,又∵AB=3,AC=2,
∴
 =
= .
.故答案为
 .
.
练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 分)
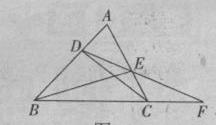
分)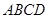 中,
中,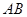 ∥
∥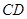 ,
,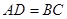 ,点
,点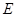 在边
在边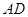 上,
上,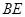 与
与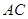 相交于点
相交于点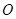 ,且
,且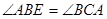 .
.
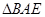 ∽
∽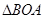 ; (6分)
; (6分)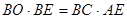 . (6分)
. (6分) ,且
,且 ,那么
,那么 ▲ .
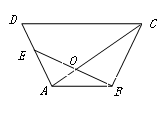
▲ . ,AC=BC,CD⊥AB于点D,点E为AC边上一点,联结BE交CD于点F,过点E作EG⊥BE交AB于点G,
,AC=BC,CD⊥AB于点D,点E为AC边上一点,联结BE交CD于点F,过点E作EG⊥BE交AB于点G,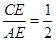 ,探究线段EF与EG的数量关系并且证明;
,探究线段EF与EG的数量关系并且证明;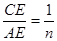 ,线段EF与EG的数量关系是 .
,线段EF与EG的数量关系是 .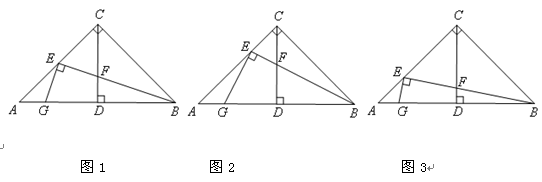
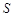 ,△ADF的面积
,△ADF的面积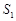 ,△PDC的面积
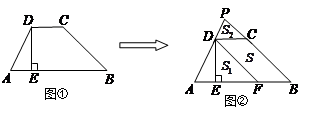
,△PDC的面积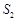 .
.
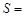 ,
,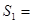 ______,
______,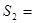 ;
;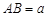 ,
,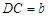 ,
,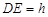 ,则
,则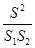 =__________,并写出理由;
=__________,并写出理由;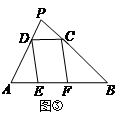

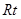 △ABC中,
△ABC中,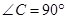 ,点
,点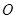 在
在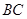 上,
上,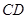 为⊙
为⊙ 于
于 ,若
,若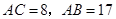 ,求⊙
,求⊙