题目内容
已知多项式A=x2-x+(3-
),若x取任何实数,A的值都不是负数,则k的取值范围是 .
| k |
| 2 |
考点:配方法的应用,非负数的性质:偶次方,解一元一次不等式
专题:
分析:根据多项式A=x2-x+(3-
),若x取任何实数,A的值都不是负数,得出△<0,再代入计算即可.
| k |
| 2 |
解答:解:∵A=x2-x+(3-
),若x取任何实数,A的值都不是负数,
∴△=(-1)2-4×1×(3-
)<0,
解得:k<
;
故答案为:k<
.
| k |
| 2 |
∴△=(-1)2-4×1×(3-
| k |
| 2 |
解得:k<
| 11 |
| 2 |
故答案为:k<
| 11 |
| 2 |
点评:此题考查了二次函数的图象和性质,关键是根据题意得出△=(-1)2-4×1×(3-
)<0,再进行求解.
| k |
| 2 |

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
3-π的相反数是( )
| A、-3-π | ||
B、
| ||
| C、3+π | ||
| D、π-3 |
 请写出点A,B,C,D,的坐标.
请写出点A,B,C,D,的坐标.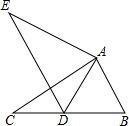 如图,在△ABC中,AB=2,BC=3.8,∠B=60°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为
如图,在△ABC中,AB=2,BC=3.8,∠B=60°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为 如图,在△ABC中,E是AB的中点,CD平分∠ACB;AD⊥CD于点D,若BC=12cm,AC=8cm.则DE=
如图,在△ABC中,E是AB的中点,CD平分∠ACB;AD⊥CD于点D,若BC=12cm,AC=8cm.则DE= 如图所示,?ABCD中,AM⊥BC于M,AN⊥CD于N,已知AB=10,BM=5,MC=3,则MN的长为
如图所示,?ABCD中,AM⊥BC于M,AN⊥CD于N,已知AB=10,BM=5,MC=3,则MN的长为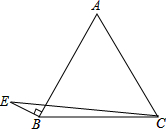 如图,已知:等边△ABC,AB=2
如图,已知:等边△ABC,AB=2 如图的运算程序中,若开始输入的x值为48,则第1次输出的结果为24,第2次输出的结果为12,…,第2014次输出的结果为
如图的运算程序中,若开始输入的x值为48,则第1次输出的结果为24,第2次输出的结果为12,…,第2014次输出的结果为