题目内容
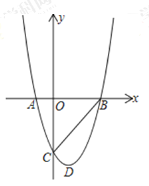
【题目】已知二次函数![]() 的图象与x轴交于A、B两点(A在B的左侧),与y轴交于点C,顶点为D.
的图象与x轴交于A、B两点(A在B的左侧),与y轴交于点C,顶点为D.
(1)画出该二次函数的图象;
(2)连接AC、CD、BD,求ABCD的面积
【答案】(1)见解析;(2)9
【解析】
(1)先求出抛物线的顶点坐标、抛物线与坐标轴的交点坐标,然后利用描点法画二次函数图象;
(2)连接OD,如图,根据三角形面积公式,利用四边形ABDC的面积=S△AOC+S△OCD+S△OBD进行计算.
解:(1)y=x2-2x-3=(x-1)2-4,
抛物线的顶点坐标为(1,-4),
解方程x2-2x-3=0,解得x1=-1,x2=3,
抛物线与x轴的交点坐标为(-1,0),(3,0),
当x=0时,y=x2-2x-3=-3,则抛物线与y轴的交点坐标为(0,-3),
如图,
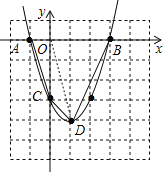
(2)连接OD,四边形ABDC的面积=S△AOC+S△OCD+S△OBD=![]() ×1×3+
×1×3+![]() ×3×1+
×3×1+![]() ×3×4=9.
×3×4=9.
故答案为9.

练习册系列答案
相关题目