题目内容
如图,在矩形ABCD中,E是CD边上任意一点(不与点C,D重合),作AF⊥AE交CB的延长线于点F.
(1)求证:△ADE∽△ABF;
(2)连接EF,M为EF的中点,AB=4,AD=2,设DE=x,
①求点M到FC的距离(用含x的代数式表示);
②连接BM,设 ,求y与x之间的函数关系式,并直接写出BM的长度的最小值.
,求y与x之间的函数关系式,并直接写出BM的长度的最小值.
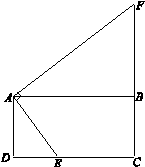
(1)证明:∵ 在矩形ABCD中,∠DAB =∠ABC =∠C =∠D =90°.
∴ 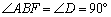 .
.
∵ AF⊥AE,
∴ ∠EAF =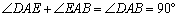 .
.
∴ 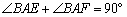 .
.
∴ ∠DAE =∠BAF.
∴ △ADE∽△ABF.
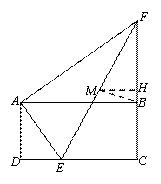 (2)解:①如图,取FC的中点H,连接MH.
(2)解:①如图,取FC的中点H,连接MH.
∵ M为EF的中点,
∴ MH∥DC ,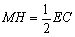 .
.
 ∵ 在矩形ABCD中,∠C =90°,
∵ 在矩形ABCD中,∠C =90°,
 ∴ MH⊥FC,即MH是点M到FC的距离.
∴ MH⊥FC,即MH是点M到FC的距离.
∵ DE=x,DC=AB=4.
∴ EC=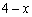 ,
,
∴ 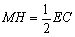
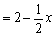 .
.
即点M到FC的距离为MH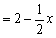 .
.
②∵△ADE∽△ABF,
∴ 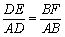 .
.
∴  .
.
∴  ,FC=
,FC=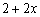 ,FH= CH=
,FH= CH= .
.
∴ 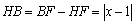 .
.
∵ 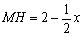 ,
,
∴ 在Rt△MHB中,
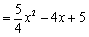 .
.
∴ 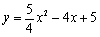 (
(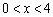 ),
),
当 时,BM长的最小值是
时,BM长的最小值是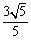 .
.

练习册系列答案
相关题目
 的图象与x轴负半轴交于点A,与y轴交于点B(0,4),已知点E(0,1).
的图象与x轴负半轴交于点A,与y轴交于点B(0,4),已知点E(0,1). A′B2+BE′2取得最小值时点E′的坐标;
A′B2+BE′2取得最小值时点E′的坐标;

 (m是常数)与直线
(m是常数)与直线 有两个交点,且这两个交点分别在抛物线对称轴的两侧,则
有两个交点,且这两个交点分别在抛物线对称轴的两侧,则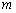 的取值范围是
的取值范围是 B.
B. C.
C. D.
D.
 .若AB=6,DC=4,PD=2,求PB的长.
.若AB=6,DC=4,PD=2,求PB的长.
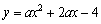
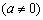 的图象与x轴交于点A,B(A点在B点的左侧),与y轴交于点C,△ABC的面积为12.
的图象与x轴交于点A,B(A点在B点的左侧),与y轴交于点C,△ABC的面积为12.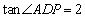 ,求点P的横坐标;
,求点P的横坐标; 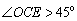 ,点O与点
,点O与点 关于EC所在直线对称.作
关于EC所在直线对称.作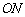 ⊥
⊥ 于点N,交EC于点M.若EM·EC=32,求点E的坐标.
于点N,交EC于点M.若EM·EC=32,求点E的坐标.
 的半径为5,
的半径为5, 为弦,
为弦, ,垂足为
,垂足为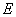 ,如果
,如果 ,那么
,那么 的长是( )
的长是( )
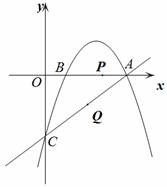
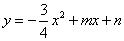 经过点A和点C,动点P在x轴上以每秒1个长度单位的速度由抛物线与x轴的另一个交点B向点A运动,点Q由点C沿线段CA向点A运动且速度是点P运动速度的2倍.
经过点A和点C,动点P在x轴上以每秒1个长度单位的速度由抛物线与x轴的另一个交点B向点A运动,点Q由点C沿线段CA向点A运动且速度是点P运动速度的2倍.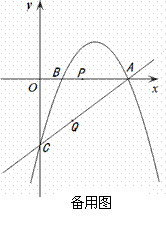 (3)在直线CA上方的抛物线上是否存在一点D,使得△ACD的面积最大.若存在,求出点D的坐标;若不存在,请说明理由.
(3)在直线CA上方的抛物线上是否存在一点D,使得△ACD的面积最大.若存在,求出点D的坐标;若不存在,请说明理由.