题目内容
(10分)如图①,正方形AEFG的边长为1,正方形ABCD的边长为3,且点F在AD上.
(1)求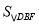 ;
;
(2)把正方形AEFG绕点A按逆时针方向旋转45°得图②,求图②中的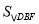 ;
;
(3)把正方形AEFG绕点A旋转一周,在旋转的过程中,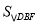 存在最大值与最小值,请直接写出最大值 ,最小值 .
存在最大值与最小值,请直接写出最大值 ,最小值 .
(1) ;(2)
;(2) ;(3)
;(3) ;
; .
.
【解析】
试题分析:(1)根据图形的关系,可得AF的长,根据三角形面积公式,可得△DBF的面积;
(2)连接AF,由题意易知AF∥BD;△DBF与△ABD同底等高,故面积相等;
(3)分析可得:当F点到BD的距离取得最大、最小值时, 取得最大、最小值.
取得最大、最小值.
试题解析:(1)∵点F在AD上, ∴ ,∴
,∴ ,
,
∴ ;
;
(2)连接DF,AF,由题意易知AF∥BD,∴四边形AFDB是梯形,∴△DBF与△ABD等高同底,即BD为两三角形的底,由AF∥BD,得到平行线间的距离相等,即高相等,∴ ;
;
(3)正方形AEFG在绕A点旋转的过程中,F点的轨迹是以点A为圆心,AF为半径的圆,存在最大值及最小值,因为△BFD的边BD= ,故当F点到BD的距离取得最大、最小值时,
,故当F点到BD的距离取得最大、最小值时, 取得最大、最小值.如图②所示DF⊥BD时,
取得最大、最小值.如图②所示DF⊥BD时, 的最大值=
的最大值= =
= =
= ,
,
 的最小值=
的最小值= =
= .
.


考点:1.旋转的性质;2.正方形的性质.

练习册系列答案
相关题目
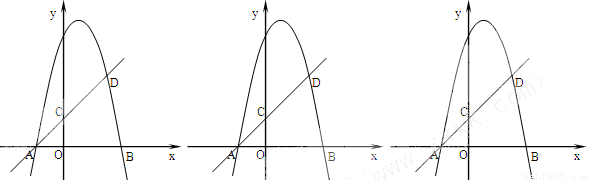

 向右平移l个单位,再向上平移2个单位后所得到的抛物线为 ( )
向右平移l个单位,再向上平移2个单位后所得到的抛物线为 ( )

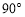 的∠MON,我们给出如下定义:若点P在∠MON的内部或边界上,作PE⊥OM于点E,PF⊥ON于点F,则称PE+PF为点P相对于∠MON的“点角距离”,记为
的∠MON,我们给出如下定义:若点P在∠MON的内部或边界上,作PE⊥OM于点E,PF⊥ON于点F,则称PE+PF为点P相对于∠MON的“点角距离”,记为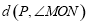 .
.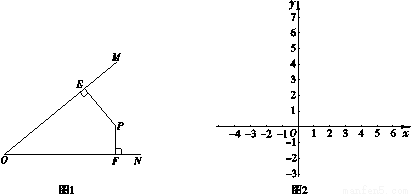
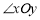 ,点P为第一象限内或两条坐标轴正半轴上的动点,且满足
,点P为第一象限内或两条坐标轴正半轴上的动点,且满足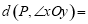 5,点P运动形成的图形记为图形G.
5,点P运动形成的图形记为图形G.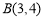 ,
,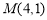 ,求
,求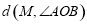 的值;
的值;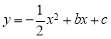 经过(2)中的A,B两点,点Q在A,B两点之间的抛物线上(点Q可与A,B两点重合),求当
经过(2)中的A,B两点,点Q在A,B两点之间的抛物线上(点Q可与A,B两点重合),求当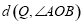 取最大值时,点Q 的坐标.
取最大值时,点Q 的坐标.