题目内容
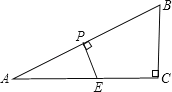
【题目】如图，在平行四边形
中，过点
作
，垂足为
，连接
，
为线段上一点，且
．
（1）求证：
；
（2）若
，
，
，求
的度数．
【答案】（1）见解析；（2）
【解析】
（1）易证∠ADF=∠CED和∠AFD=DCE，即可证明△ADF∽△DEC．
（2）根据平行四边形对边相等可求得CD的长，根据△ADF∽△DEC，利用对应边成比例即可求得DE的长，
（1）∵平行四边形ABCD中，AB∥CD，AD∥BC，
∴∠B+∠DCE=180°，∠ADF=∠CED，
∵∠B=∠AFE，∠AFD+∠AFE=180°，
∴∠AFD=∠DCE，
∴△ADF∽△DEC；
（2）∵四边形ABCD为平行四边形，
∴CD=AB=8，AD∥BC，
，
∴AE⊥AD，
∵△ADF∽△DEC，
∴
，即
，
∴DE=12，
∵在Rt△ADE中，∠EAD=90°，
，DE=12，
∴
，
∵
，
∴．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
【题目】每个人都应怀有对水的敬畏之心，从点滴做起，节水、爱水，保护我们生活的美好世界．某地近年来持续干旱，为倡导节约用水，该地采用了“阶梯水价”计费方法，具体方法：每户每月用水量不超过4吨的每吨2元；超过4吨而不超过6吨的，超出4吨的部分每吨4元；超过6吨的，超出6吨的部分每吨6元．该地一家庭记录了去年12个月的月用水量如下表，下列关于用水量的统计量不会发生改变的是（ ）
用水量x（吨） | 3 | 4 | 5 | 6 | 7 |
频数 | 1 | 2 | 5 | 4﹣x | x |
A. 平均数、中位数 B. 众数、中位数 C. 平均数、方差 D. 众数、方差
