题目内容
已知正比例函数y=(2m-1)x的图象上两点A(x1,y1),B(x2,y2),当x1<x2时,有y1>y2,则m的取值范围是 .
考点:一次函数图象上点的坐标特征
专题:计算题
分析:根据一次函数图象上点的坐标特征得到y1=(2m-1)x1,y2=(2m-1)x2,由于x1<x2时,y1>y2,则2m-1<0,然后解不等式即可.
解答:解:∵正比例函数y=(2m-1)x的图象上两点A(x1,y1),B(x2,y2),
∴y1=(2m-1)x1,y2=(2m-1)x2,
∵x1<x2时,y1>y2,
∴2m-1<0,
∴m<
.
故答案为m<
.
∴y1=(2m-1)x1,y2=(2m-1)x2,
∵x1<x2时,y1>y2,
∴2m-1<0,
∴m<
| 1 |
| 2 |
故答案为m<
| 1 |
| 2 |
点评:本题考查了一次函数图象上点的坐标特征:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(-bk,0);与y轴的交点坐标是(0,b).直线上任意一点的坐标都满足函数关系式y=kx+b.

练习册系列答案
相关题目
 如图是一个正方体的表面展开图,上面标有“我、爱、鲁、能、巴、蜀”六个字,图中“我”对面的字是( )
如图是一个正方体的表面展开图,上面标有“我、爱、鲁、能、巴、蜀”六个字,图中“我”对面的字是( )| A、鲁 | B、能 | C、巴 | D、蜀 |
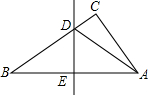 如图,在△ABC中,边AB的垂直平分线分别交BC、AB于点D、E,AE=3cm,BD=5cm,则△ABD的周长是( )
如图,在△ABC中,边AB的垂直平分线分别交BC、AB于点D、E,AE=3cm,BD=5cm,则△ABD的周长是( )| A、8cm | B、11cm |
| C、13cm | D、16cm |
下列运算正确的是( )
| A、x+y=xy |
| B、5x3-2x3=3 |
| C、x2+3x3=4x5 |
| D、5x2y-4x2y=x2y |
 如图,⊙O的直径CD与弦AB垂直相交于点E,且BC=1,AD=2,求⊙O的直径长.
如图,⊙O的直径CD与弦AB垂直相交于点E,且BC=1,AD=2,求⊙O的直径长. 如图,一条直线AD分别与直线BE、CE、CF相交于A、G、H、D,且∠1=∠2,∠A=∠D.求证:∠B=∠C.
如图,一条直线AD分别与直线BE、CE、CF相交于A、G、H、D,且∠1=∠2,∠A=∠D.求证:∠B=∠C.