题目内容
20.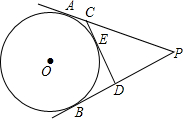 如图,PA、PB切⊙O于点A、B,CD是⊙O的切线,交PA、PB于C、D两点,△PCD的周长是36,则AP的长为( )
如图,PA、PB切⊙O于点A、B,CD是⊙O的切线,交PA、PB于C、D两点,△PCD的周长是36,则AP的长为( )| A. | 12 | B. | 18 | C. | 24 | D. | 9 |
分析 由于DA、DC、BC都是⊙O的切线,可根据切线长定理,将△PCD的周长转换为PA、PB的长,然后再进行求解即可.
解答 解:
∵PA、PB分别是⊙O的切线,且切点为A、B;
∴PA=PB;
同理,可得:DE=DA,CE=CB;
则△PCD的周长=PD+DE+CE+PC=PD+DA+PC+CB=PA+PB=36,
∴PA=PB=18,
故选B.
点评 此题主要考查了切线长定理的应用,能够将△PCD的周长转换为切线PA、PB的长是解答此题的关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
12.下列说法中正确的是( )
| A. | 近似数0.66有两个有效数字 | B. | 近似数5.01×103精确到百分位 | ||
| C. | 近似数2.10精确到十分位 | D. | 近似数5.8万精确到万位 |
9. 如图,在长为100m,宽为80m的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面积为7644m2,则道路的宽应为多少米?设道路的宽为x m,则可列方程为( )
如图,在长为100m,宽为80m的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面积为7644m2,则道路的宽应为多少米?设道路的宽为x m,则可列方程为( )
 如图,在长为100m,宽为80m的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面积为7644m2,则道路的宽应为多少米?设道路的宽为x m,则可列方程为( )
如图,在长为100m,宽为80m的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面积为7644m2,则道路的宽应为多少米?设道路的宽为x m,则可列方程为( )| A. | 100×80-100x-80x=7644 | B. | (100-x)(80-x)+x2=7644 | ||
| C. | (100-x)(80-x)=7644 | D. | 100x+80x-x2=7644 |
10.下列四个实数中,最大的是( )
| A. | -2 | B. | 0 | C. | -$\sqrt{2}$ | D. | $\sqrt{3}$ |
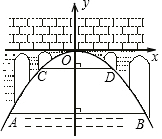 有一座抛物线形拱桥,校下面在正常水位时AB宽20米,水位上升3米就达到警戒线CD,这时水面宽度为10米.
有一座抛物线形拱桥,校下面在正常水位时AB宽20米,水位上升3米就达到警戒线CD,这时水面宽度为10米.