题目内容
如图：A，B是函数y=
的图象上关于原点O对称的任意两点．AC平行于y轴，BC平行于x轴，求△ABC的面积．
| 1 |
| x |
如图所示，
设A点坐标为（x、
），则B点坐标为（-x，-
），
∴C点坐标为（x，-
），
∴S矩形OECD=x•|-
|=1，
∵A、B为函数y=
图象上两点，
∴S△AOE=S△BOD=
k=
，
∴S△ABC=S矩形OECD+S△AOE+S△BOD=1+
+
=2．
设A点坐标为（x、
| 1 |
| x |
| 1 |
| x |
∴C点坐标为（x，-
| 1 |
| x |
∴S矩形OECD=x•|-
| 1 |
| x |
∵A、B为函数y=
| 1 |
| x |
∴S△AOE=S△BOD=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ABC=S矩形OECD+S△AOE+S△BOD=1+
| 1 |
| 2 |
| 1 |
| 2 |
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
的图象交于A、B两点，过点A作AM⊥x轴，垂足为M，连结BM,若
=3，则k的值是 .
（k >0）的图象与经过原点的直线l相交于A、B两点，已知A点的坐标为（2，1），那么B点的坐标为 ．
—
+
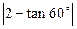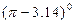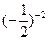
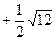
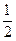时，y的值．
