题目内容
14.小明说在实数范围内代数式3x2+6x+10的值和代数式2x2-1的值不可能相等.你认为小明的结论正确吗?为什么?分析 把两个式子相减等于0,如果能求得x的数值,则两个式子相等,否则不可.
解答 解:小明的结论正确.
假设相等,
则3x2+6x+10-(2x2-1)=0
x2+6x+11=0,
(x+3)2+2=0
∵(x+3)2≥0,
∴>0,
∴假设不成立,也就是在实数范围内代数式3x2+6x+10的值和代数式2x2-1的值不可能相等.
点评 此题考查配方法的运用,掌握完全平方公式和非负数的性质是关键.

练习册系列答案
相关题目
5.若方程2x2-4x-k=0有两个相等的实数根,则k的值为( )
| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
9.填写下表:
上表中已知数a的小数点的移动与它的立方根$\root{3}{a}$的小数点的移动有何规律?这个规律用倍数关系的语言怎样叙述?
| a | 0.000001 | 0.001 | 1 | 1000 | 1000000 |
| $\root{3}{a}$, | 0.01 | 0.1 | 1 | 10 | 100 |
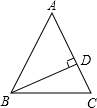 如图,在△ABC中,AB=AC,BD⊥AC,D是垂足,DC=4,cosA=$\frac{3}{5}$,求tanC的值.
如图,在△ABC中,AB=AC,BD⊥AC,D是垂足,DC=4,cosA=$\frac{3}{5}$,求tanC的值. 的两个解是
的两个解是 和
和
 、
、 的值;
的值; 的代数式表示
的代数式表示 ;
; 是不小于
是不小于 的负数,求
的负数,求 的取值范围.
的取值范围.