��Ŀ����
����Ŀ���ۺ���̽��
���ⱳ��
���ۺ�ʵ�����ϣ���ʦ��ͬѧ�Ǹ������������龳��д��������ѧ���ۣ�
��ͼ����C���߶�BD�ϣ���E���߶�AC�ϣ���ACB����ACD��90�㣬AC��BC��DC��CE��M��N�ֱ����߶�BE��AD�ϵĵ㣮
����ȤС�顱д����������ѧ�����ǣ��١�BCE�ա�ACD���ڵ�CM��CN�ֱ��ǡ�BCE�͡�ACD������ʱ����MCN�ǵ���ֱ�������Σ�
�������
��1��������ͼ��1����֤������ȤС�顱��д���������۵���ȷ�ԣ�
���̽��
�ܵ�����ȤС�顱����������ʵ��С�顱��ͬѧ��д�����½��ۣ���ͼ��2��������BCM����ACNʱ����MCN�ǵ���ֱ�������Σ�
��2����ʵ��С�顱��д�Ľ����Ƿ���ȷ����˵�����ɣ�
������
���ܽ�С�顱��Ϊ������M��N�ֱ���BE��AD�����ȷֵ�ʱ����MCN��Ȼ�ǵ���ֱ������������˼����
��3�����ܽ�С�顱��������Ƿ���ȷ������ �������ȷ����������ȷ����һ����ȷ������
��4����˼�����̽�����̣����������ʵ�����������д��ʹ�á�MCN�ǵ���ֱ�������ε���ѧ���ۣ�����д���۱�����ȷ��д��1�����ɣ���Ҫ��֤����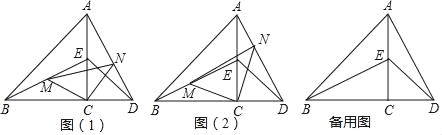
���𰸡���1������������2��ʵ��С�顱��д�Ľ�����ȷ�����ɼ���������3����һ��ȷ�����ɼ���������4���𰸲�Ψһ��������
��������
��1������BCE�ա�ACD���Ƴ�BE��AD����EBC����DAC����ΪBM��![]() BE��AN��
BE��AN��![]() AD���Ƴ�BM��AN����֤����BCM�ա�ACN�����ɽ�����⣻
AD���Ƴ�BM��AN����֤����BCM�ա�ACN�����ɽ�����⣻
��2��ʵ��С�顱��д�Ľ�����ȷ��ֻҪ֤����BCM�ա�ACN��ASA�������ɽ�����⣻
��3�����ܽ�С�顱��Ϊ������M��N�ֱ���BE��AD�����ȷֵ�ʱ����MCN��Ȼ�ǵ���ֱ�������Σ�������۲�һ��ȷ������������˵�����ɣ�
��4���𰸲�Ψһ�����磺��CM��CN�ֱ�����BCE����ACD�ĸ�ʱ����MCN�ǵ���ֱ�������Σ���CM��CN�ֱ�����BCE����ACD�Ľ�ƽ����ʱ����MCN�ǵ���ֱ��������.
��1������BCE����ACD��
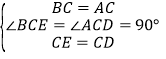 ��
��
���BCE����ACD��SAS����
��BE��AD����EBC����DAC��
��CM��CN�ֱ�����BCE����ACD�����ߣ�
��BM��![]() BE��AN��
BE��AN��![]() AD��
AD��
��BM��AN��
����BCM����ACN��
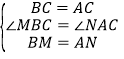 ��
��
���BCM�ա�ACN��SAS����
��CM��CN����BCM����ACN��
�ߡ�BCM+��MCE��90�㣬
���ACN+��MCE��90�㣬
��MC��CN��
���MCN�ǵ���ֱ�������Σ�
��2��ʵ��С�顱��д�Ľ�����ȷ��
���ɣ��ߡ�BCE�ա�ACD��
���EBC����DAC��
����BCM����CAN��
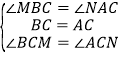 ��
��
��BCM�ա�ACN��ASA����
��CM��CN��
�ߡ�BCM+��MCE����ACB��90�㣬
���ACN+��MCE��90�㣬
��MC��CN��
���MCN�ǵ���ֱ�������Σ�
��3�����ܽ�С�顱��Ϊ������M��N�ֱ���BE��AD�����ȷֵ�ʱ����MCN��Ȼ�ǵ���ֱ�������Σ�������۲�һ��ȷ��
���ɣ���BM��![]() BE��AN��
BE��AN��![]() ADʱ����MCN��Ȼ�ǵ���ֱ�������Σ�
ADʱ����MCN��Ȼ�ǵ���ֱ�������Σ�
��BM��![]() BE��DN��
BE��DN��![]() ADʱ����MCN���ǵ���ֱ�������Σ�
ADʱ����MCN���ǵ���ֱ�������Σ�
�ʴ�Ϊ��һ��ȷ��
��4���𰸲�Ψһ�����磺��CM��CN�ֱ�����BCE����ACD�ĸ�ʱ����MCN�ǵ���ֱ�������Σ�
��CM��CN�ֱ�����BCE����ACD�Ľ�ƽ����ʱ����MCN�ǵ���ֱ�������Σ�
���ɣ�ֻҪ֤����BCM�ա�ACN��AAS���������Ƴ�����BCM����ACN���Ƴ���MCN��90�㣬
��CM��CN��
���MCN�ǵ���ֱ�������Σ�

����Ŀ��ij�̳�Ͷ��13 800Ԫ�ʽ��ס������ֿ�Ȫˮ��500�䣬��Ȫˮ�ijɱ��ۺ����ۼ������ʾ��
���/���� | �ɱ��� | ���ۼ�(Ԫ/��) |
�� | 24 | 36 |
�� | 33 | 48 |
(1)���̳������ס������ֿ�Ȫˮ�������䣿
(2)ȫ������500���Ȫˮ�����̳�������������Ԫ��