题目内容
填空：
（a﹣b）（a+b）= ；
（a﹣b）（a2+ab+b2）= ；
（a﹣b）（a3+a2b+ab2+b3）= ．
（2）猜想：
（a﹣b）（an﹣1+an﹣2b+…
+abn﹣2+bn﹣1）= （其中n为正整数
，且n≥2）．
（3）利用（2）猜想的结论计算：
29﹣28+27﹣…+23﹣22+2．
解：（1）（a﹣b）（a+b）=a2﹣b2；
（a﹣b）（a2+ab+b2）=a3+a2b+ab2﹣a2b﹣ab2﹣b3=a3﹣b3；
（a﹣b）（a3+a2b+ab2+b3）=a4+a3b+a2b2+ab3﹣a3b﹣a2b2﹣ab3﹣b4=a4﹣b4；
故答案为：a2﹣b2，a3﹣b3，a4﹣b4；
（2）由（1）的规律可得：
原式=an﹣bn，
故答案为：an﹣bn；
（3）29﹣28+27﹣…+23﹣22+2=（2﹣1）（28+26+24+22+2）=342．
学练快车道快乐假期寒假作业系列答案
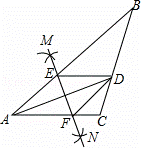
新思维寒假作业系列答案如图，在△ABC中，AD平分∠BAC，按如下步骤作图：
第一步，分别以点A、D为圆心，以大于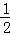
AD的长为半径在AD两侧作弧，交于两点M、N；
第二步，连接MN分别交AB、AC于点E、F；
第三步，连接DE、DF．
若BD=6，AF=4，CD=3，则BE的长是（ ）
|
| A． | 2 | B． | 4 | C． | 6 | D． | 8 |
调k（0＜k＜100）元，若商店保持这两种家电的售价不变，请你根据以上信息及（2）问中条件，设计出使这100台家电销售总利润最大的进货方案．2011年3月，英国和新加坡研究人员制造出观测极限为0.000 000 05米的光学显微镜，其中0.000 000 05米用科学记数法表示正确的是（ ）
|
| A． | 0.5×10﹣9米 | B． | 5×10﹣8米 | C． | 5×10﹣9米 | D． | 5×10﹣7米 |
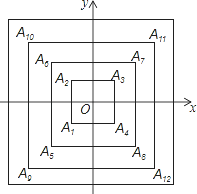
如图，在矩形ABCD中，已知AB=4，BC=3，矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位置，再绕右下角的顶点继续向右旋转90°至图②位置，…，以此类推，这样连续旋转2015次后，顶点A在整个旋转过程中所经过的路程之和是（ ）
|
| A． | 2015π | B． | 3019.5π | C． | 3018π | D． | 3024π |
+1）
，其中a=
；