题目内容
已知 ,
, ,求x2+y2+z2-xy-yz-xz的值.
,求x2+y2+z2-xy-yz-xz的值.
解:∵ ,
, ,
,
∴x-z= ,
,
x2+y2+z2-xy-yz-xz
= ×(2x2+2y2+2z2-2xy-2yz-2xz)
×(2x2+2y2+2z2-2xy-2yz-2xz)
= ×[(x-y)2+(y-z)2+(x-z)2]
×[(x-y)2+(y-z)2+(x-z)2]
= ×[(
×[( )2+(
)2+(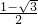 )2+(
)2+( )2]
)2]
= ×[1+
×[1+ +1-
+1- +3]
+3]
= ×5
×5
=2.5.
分析:由 ,
, ,易得x-z=
,易得x-z= ,然后把x2+y2+z2+xy-yz+xz进行变形得到x2+y2+z2-xy-yz-xz=
,然后把x2+y2+z2+xy-yz+xz进行变形得到x2+y2+z2-xy-yz-xz= (2x2+2y2+2z2-2xy-2yz-2xz),根据完全平方公式有原式=
(2x2+2y2+2z2-2xy-2yz-2xz),根据完全平方公式有原式= [(x-y)2+(y-z)2+(x-z)2],再代值计算即可.
[(x-y)2+(y-z)2+(x-z)2],再代值计算即可.
点评:本题考查了完全平方公式:(a±b)2=a2±2ab+b2.也考查了代数式的变形能力.
 ,
, ,
,∴x-z=
 ,
,x2+y2+z2-xy-yz-xz
=
 ×(2x2+2y2+2z2-2xy-2yz-2xz)
×(2x2+2y2+2z2-2xy-2yz-2xz)=
 ×[(x-y)2+(y-z)2+(x-z)2]
×[(x-y)2+(y-z)2+(x-z)2]=
 ×[(
×[( )2+(
)2+(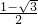 )2+(
)2+( )2]
)2]=
 ×[1+
×[1+ +1-
+1- +3]
+3]=
 ×5
×5=2.5.
分析:由
 ,
, ,易得x-z=
,易得x-z= ,然后把x2+y2+z2+xy-yz+xz进行变形得到x2+y2+z2-xy-yz-xz=
,然后把x2+y2+z2+xy-yz+xz进行变形得到x2+y2+z2-xy-yz-xz= (2x2+2y2+2z2-2xy-2yz-2xz),根据完全平方公式有原式=
(2x2+2y2+2z2-2xy-2yz-2xz),根据完全平方公式有原式= [(x-y)2+(y-z)2+(x-z)2],再代值计算即可.
[(x-y)2+(y-z)2+(x-z)2],再代值计算即可.点评:本题考查了完全平方公式:(a±b)2=a2±2ab+b2.也考查了代数式的变形能力.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 ,
, ,求x2-y2的值.
,求x2-y2的值. ,
, ,求x2-y2的值.
,求x2-y2的值. ,
, ,求x2-y2的值.
,求x2-y2的值.