Question

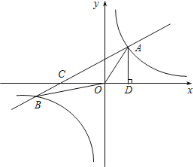
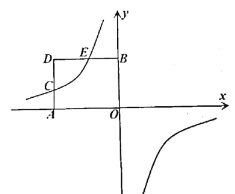
【题目】如图，在平面直角坐标系中，已知矩形的顶点，过点的双曲线与矩形的边交于点．

(1)求双曲线的解析式以及点的坐标；．

(2)若点是抛物线的顶点；

①当双曲线过点时，求顶点的坐标；

②直接写出当抛物线过点时，该抛物线与矩形公共点的个数以及此时的值．

Answer 1

【答案】（1），；（2）①；②三个，

【解析】

（1）将C点坐标代入求得k的值即可求得反比例函数解析式，将代入所求解析式求得x的值即可求得E点坐标；

（2）①将抛物线化为顶点式，可求得P点的横坐标，再根据双曲线解析式即可求得P点坐标；②根据B点为函数与y轴的交点可求得t的值和函数解析式，再根据函数的对称轴，与x轴的交点坐标即可求得抛物线与矩形公共点的个数．

解:(1)把点代入，得，

∴

把代入，得，

∴；

(2)①∵抛物线

∴顶点的横坐标，

∵顶点在双曲线上，

∴，

∴顶点，

②当抛物线过点时，

，解得，

抛物线解析式为，

故函数的顶点坐标为，对称轴为，与x轴的交点坐标分别为

所以它与矩形在线段BD上相交于和，在线段AB上相交于，即它与矩形有三个公共点，此时．