题目内容
18.若二次函数y=ax2+bx+c的x与y的部分对应值如下表:| x | -7 | -6 | -5 | -4 | -3 | -2 |
| y | -27 | -13 | -3 | 3 | 5 | 3 |
分析 取三组对应值(-4,3)、(-3,5)、(-2,3)代入y=ax2+bx+c得到关于a、b、c的方程组,然后解方程组求出a、b、c的值,从而得到抛物线解析式.
解答 解:把(-4,3)、(-3,5)、(-2,3)代入y=ax2+bx+c得$\left\{\begin{array}{l}{16a-4b+c=3}\\{9a-3b+c=5}\\{4a-2b+c=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-2}\\{b=-12}\\{c=-13}\end{array}\right.$.
所以抛物线解析式为y=-2x2-12x-13.
故答案为y=-2x2-12x-13.
点评 本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
13.2012年全年国内生产总值519000亿元,用科学记数法表示( )亿元.
| A. | 0.519×106 | B. | 5.19×105 | C. | 5.19×106 | D. | 0.519×105 |
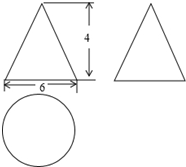 已知一个几何体的三视图如图所示,
已知一个几何体的三视图如图所示, 画出下图四棱柱的主视图、左视图和俯视图.
画出下图四棱柱的主视图、左视图和俯视图.