题目内容
2.解方程组$\left\{\begin{array}{l}{x-y+1=0}\\{{x}^{2}-4xy+4{y}^{2}-4=0}\end{array}\right.$.分析 用代入法即可解答,即把①化为x=y-1,把x=y-1代入②得关于y的一元二次方程,解方程求出y,把y代入x=y-1求出x即可.
解答 解:$\left\{\begin{array}{l}{x-y+1=0①}\\{{x}^{2}-4xy+4{y}^{2}=4②}\end{array}\right.$
由①得,x=y-1③,
把③代入②得:(y-1)2-4(y-1)×y+4y2=4,
即y2+2y-3=0,
解得:y1=1,y2=-3,
把y1=1,y2=-3代入①得,
x1=0,x2=-4,
故原方程组的解为:$\left\{\begin{array}{l}{{x}_{1}=0}\\{{y}_{1}=1}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-4}\\{{y}_{2}=-3}\end{array}\right.$.
点评 本题考查的是二元二次方程组的解法,把二元一次方程变形,即用一个未知数表示另一个未知数,代入二元二次方程,得到一个一元二次方程,再解关于另一个未知数的一元二次方程,把求得结果代入一个较简单的方程中解方程即可.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
13. 如图,抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于C点,若∠OBC=45°,则下列各式成立的是( )
如图,抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于C点,若∠OBC=45°,则下列各式成立的是( )
 如图,抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于C点,若∠OBC=45°,则下列各式成立的是( )
如图,抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于C点,若∠OBC=45°,则下列各式成立的是( )| A. | b+c-1=0 | B. | b+c+1=0 | C. | b-c+1=0 | D. | b-c-1=0 |
11. 如图,直线AB、CD被直线EF所截,AB∥CD,∠1=100°,则∠2等于( )
如图,直线AB、CD被直线EF所截,AB∥CD,∠1=100°,则∠2等于( )
 如图,直线AB、CD被直线EF所截,AB∥CD,∠1=100°,则∠2等于( )
如图,直线AB、CD被直线EF所截,AB∥CD,∠1=100°,则∠2等于( )| A. | 70° | B. | 80° | C. | 90° | D. | 100° |
12.下列计算正确的是( )
| A. | 2a2•2a2=4a2 | B. | 2x3•2x3=2x9 | C. | x•y=(xy)2 | D. | (-3x)2=9x2 |
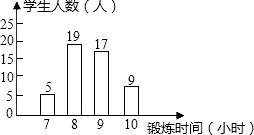 如图是根据某班50名同学一周的体育锻炼情况绘制的条形统计图,则这个班50名同学一周参加体育锻炼时间的众数是8小时,中位数是9小时.
如图是根据某班50名同学一周的体育锻炼情况绘制的条形统计图,则这个班50名同学一周参加体育锻炼时间的众数是8小时,中位数是9小时.