题目内容
13. 如图,抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于C点,若∠OBC=45°,则下列各式成立的是( )
如图,抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于C点,若∠OBC=45°,则下列各式成立的是( )| A. | b+c-1=0 | B. | b+c+1=0 | C. | b-c+1=0 | D. | b-c-1=0 |
分析 根据∠OBC=45°,有OB=OC,可设点C,B的坐标为(0,c),(c,0),把点B(c,0)代入二次函数y=x2+bx+c,得c2+bc+c=0,从而求出关系式.
解答 解:∵∠OBC=45°,
∴OB=OC,
∴点C,B的坐标为(0,c),(c,0);
把点B(c,0)代入二次函数y=x2+bx+c,得c2+bc+c=0,
即c(c+b+1)=0,
∵c≠0,
∴b+c+1=0.
故选:B.
点评 此题考查了抛物线与x轴的交点.根据题意得到点C、B的坐标是解题的关键.

练习册系列答案
相关题目
4.使$\frac{\sqrt{x-1}}{2}$有意义的x的取值范围是( )
| A. | x>1 | B. | x≥1 | C. | x<1 | D. | x≤1 |
8. 如图,已知AB∥CD,∠A=60°,则∠CEF的度数为( )
如图,已知AB∥CD,∠A=60°,则∠CEF的度数为( )
 如图,已知AB∥CD,∠A=60°,则∠CEF的度数为( )
如图,已知AB∥CD,∠A=60°,则∠CEF的度数为( )| A. | 140° | B. | 120° | C. | 100° | D. | 80° |
5.下列计算正确的是( )
| A. | a4+a4=a8 | B. | 3(a-2b)=3a-2b | C. | a5÷a3=a2 | D. | (2a-b)2=4a2-b2 |
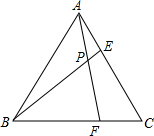 等边三角形ABC的边长为6,在AC,BC边上各取一点E、F,连接AF,BE相交于点P,若AE=CF,则∠APB=120°.
等边三角形ABC的边长为6,在AC,BC边上各取一点E、F,连接AF,BE相交于点P,若AE=CF,则∠APB=120°.