题目内容
 如图:△ABC的两个外角平分线交于点P,则下列结论正确的是
如图:△ABC的两个外角平分线交于点P,则下列结论正确的是
①PA=PC ②BP平分∠ABC ③P到AB,BC的距离相等 ④BP平分∠APC.
- A.①②
- B.①④
- C.③②
- D.③④
C
分析:根据角平分线上的点到角的两边的距离相等,过点P作PD⊥BA与点D,PE⊥AC于点E,PF⊥BC于点F,则PD=PE=PF.点P在∠ABC的平分线上.
解答: 解:过点P作PD⊥BA与点D,PE⊥AC于点E,PF⊥BC于点F.
解:过点P作PD⊥BA与点D,PE⊥AC于点E,PF⊥BC于点F.
∵AP平分∠DAE,CP平分∠ACF,
∴PD=PE=PF.
∴点P在∠ABC的平分线上,P到AB,BC的距离相等.
故②③正确.
故选C.
点评:此题考查角平分线的性质:角平分线上的点到角的两边的距离相等;到角的两边距离相等的点在角的平分线上.
分析:根据角平分线上的点到角的两边的距离相等,过点P作PD⊥BA与点D,PE⊥AC于点E,PF⊥BC于点F,则PD=PE=PF.点P在∠ABC的平分线上.
解答:
 解:过点P作PD⊥BA与点D,PE⊥AC于点E,PF⊥BC于点F.
解:过点P作PD⊥BA与点D,PE⊥AC于点E,PF⊥BC于点F.∵AP平分∠DAE,CP平分∠ACF,
∴PD=PE=PF.
∴点P在∠ABC的平分线上,P到AB,BC的距离相等.
故②③正确.
故选C.
点评:此题考查角平分线的性质:角平分线上的点到角的两边的距离相等;到角的两边距离相等的点在角的平分线上.

练习册系列答案
相关题目
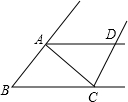 如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )
如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )| A、60° | B、80° | C、65° | D、40° |
 5、如图:△ABC的两个外角平分线交于点P,则下列结论正确的是( )
5、如图:△ABC的两个外角平分线交于点P,则下列结论正确的是( ) 物线y=a(x+5)2+k过A、B、C三点.
物线y=a(x+5)2+k过A、B、C三点. 如图,△ABC的两个外角平分线交于D点,若∠D=65゜,则∠B等于( )
如图,△ABC的两个外角平分线交于D点,若∠D=65゜,则∠B等于( )