题目内容
2.金堂有“花园水城”之称,某校就同学们对“金堂历史文化”的了解程度进行随机抽样调查,将调查结果绘制成如下两幅统计图: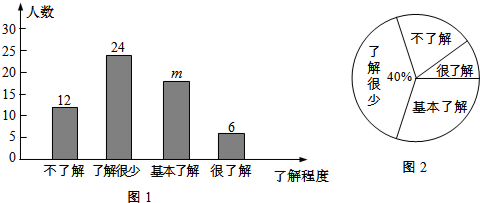
根据统计图的信息,解答下列问题:
(1)本次共凋查60名学生,条形统计图中m=18;
(2)若该校共有学生1200名,则该校约有名学生不了解“金堂历史文化”;
(3)调查结果中,该校九年级(2)班学生中了解程度为“很了解”的同学进行测试,发现其中有四名同学相当优秀,他们是三名男生、一名女生,现准备从这四名同学中随机抽取两人去市里参加“金堂历史文化”知识竞赛,用树状图或列表法,求恰好抽中一男生一女生的概率.
分析 (1)根据了解很少的有24人,占40%,即可求得总人数;利用调查的总人数减去其它各项的人数即可求得m的值;
(2)利用1200乘以不了解“金堂历史文化”的人所占的比例即可求解;
(3)列出表格即可求出恰好抽中一男生一女生的概率.
解答 解:(1)由题目图表提供的信息可知总人数=24÷40%=60(人),
m=60-12-24-6=18,
故答案为:60,18;
(2)1200×$\frac{12}{60}$=240(人),
答:该校约有240名学生不了解“金堂历史文化”;
(3)列表如下:
男 | 男 | 男 | 女 | |
| 男 | (男,男) | (男,男) | (男,女) | |
| 男 | (男,男) | (男,男) | (男,女) | |
| 男 | (男,男) | (男,男) | (男,女) | |
| 女 | (女,男) | (女,男) | (女,男) |
∴P(一男一女)=$\frac{6}{12}$=$\frac{1}{2}$.
点评 本题考查的是条形统计图和扇形统计图的综合运用以及求随机事件的概率,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.若(x+a)(x-b)=x2+mx+n,则m,n的值分别是( )
| A. | m=a-b,n=ab | B. | m=-(a-b),n=ab | C. | m=a-b,n=-ab | D. | m=-(a-b),n=-ab |
10.一元二次方程x2+x+$\frac{1}{3}$=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 无实数根 | D. | 无法确定 |
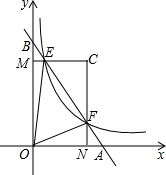 如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于A,B与反比例函数y=$\frac{k}{x}$(k>0且为常数)在第一象限的图象交于点E,F,过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C,若$\frac{BE}{BF}$=$\frac{2}{5}$,则$\frac{{S}_{△CEF}}{{S}_{△OEF}}$=$\frac{3}{7}$.
如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于A,B与反比例函数y=$\frac{k}{x}$(k>0且为常数)在第一象限的图象交于点E,F,过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C,若$\frac{BE}{BF}$=$\frac{2}{5}$,则$\frac{{S}_{△CEF}}{{S}_{△OEF}}$=$\frac{3}{7}$. 如图,∠1还可以用∠BCE表示,若∠1=62°9′36″,那么62°9′36″=62.16度.
如图,∠1还可以用∠BCE表示,若∠1=62°9′36″,那么62°9′36″=62.16度.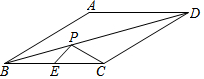 已知点E是菱形ABCD边BC上的中点,∠ABC=30°,P是对角线BD上一点,且PC+PE=$\sqrt{26}$.则菱形ABCD面积的最大值是20+8$\sqrt{3}$.
已知点E是菱形ABCD边BC上的中点,∠ABC=30°,P是对角线BD上一点,且PC+PE=$\sqrt{26}$.则菱形ABCD面积的最大值是20+8$\sqrt{3}$.