题目内容
17.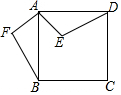 如图,点E是正方形ABCD内的一点,将△ADE绕点A顺时针旋转90°至△ABF.
如图,点E是正方形ABCD内的一点,将△ADE绕点A顺时针旋转90°至△ABF.(1)直接写出图中一组相等的线段和一组相等的角.
(2)若∠ADE=35°,∠DAE=50°,求∠F的度数.
(3)若连接EF,则△AEF是等腰直角三角形.
分析 (1)利用旋转不变性即可解决问题;
(2)在△ADE中,求出∠E即可解决问题;
(3)△AEF是等腰直角三角形;
解答 解:(1)由旋转不变性可知:AE=AF,∠ADE=∠ABF.
(2)∵∠EAD+∠ADE+∠E=180°,∠ADE=35°,∠DAE=50°,
∴∠E=180°-35°-50°=95°,
由旋转不变性可知:∠F=∠E=95°.
(3)连接EF.
∵AF=AE,∠EAF=90°,
∴△AEF是等腰直角三角形,
故答案为等腰直角.
点评 本题考查旋转的性质、正方形的性质、三角形的内角和定理、等腰直角三角形的判定等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
5.已知p,q是方程x2-3x-1=0的两根,且p>q,则p2-q2的值是( )
| A. | $\sqrt{13}$ | B. | -$\sqrt{13}$ | C. | 3$\sqrt{13}$ | D. | -3$\sqrt{13}$ |
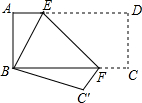 如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,△BC′F的周长是3.
如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,△BC′F的周长是3.