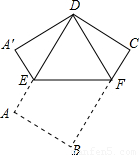
题目内容
 将矩形纸片ABCD如图那样折叠,使顶点B与顶点D重合,折痕为EF.若AB=
将矩形纸片ABCD如图那样折叠,使顶点B与顶点D重合,折痕为EF.若AB= ,AD=3,则四边形A′EFD的周长为________.
,AD=3,则四边形A′EFD的周长为________.
5+
分析:根据题意A′E=AE,A′D=AB,BF=DF,所以在Rt△A′ED中,设A′E=x,根据勾股定理可求得x=1,则DE=2,同理在Rt△DCF中,设CF=x,根据勾股定理可求得x=1,BF=2.作EG⊥BF,再根据勾股定理可得EF=2,所以四边形A′EFD的周长为1+ +2+2=5+
+2+2=5+ .
.
解答: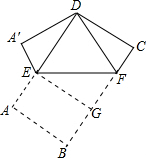 解:在Rt△A′ED中,设A′E=x,
解:在Rt△A′ED中,设A′E=x,
根据勾股定理x2+ =(3-x)2,
=(3-x)2,
解得x=1,即A′E=1;
同理在Rt△DCF中,设CF=x,根据勾股定理可求得x=1,即CF=1;
作EG⊥BF,则EG=AB= ,FG=AD-AE-CF=3-1-1=1,
,FG=AD-AE-CF=3-1-1=1,
∴EF=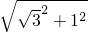 =2,
=2,
∴四边形A′EFD的周长=1+ +2+2=5+
+2+2=5+ .
.
故答案为5
点评:本题除了用到了翻折变换外,还多次用到了勾股定理.在几何中勾股定理是常用的一个定理,所以学生一定要熟练掌握.

分析:根据题意A′E=AE,A′D=AB,BF=DF,所以在Rt△A′ED中,设A′E=x,根据勾股定理可求得x=1,则DE=2,同理在Rt△DCF中,设CF=x,根据勾股定理可求得x=1,BF=2.作EG⊥BF,再根据勾股定理可得EF=2,所以四边形A′EFD的周长为1+
 +2+2=5+
+2+2=5+ .
.解答:
 解:在Rt△A′ED中,设A′E=x,
解:在Rt△A′ED中,设A′E=x,根据勾股定理x2+
 =(3-x)2,
=(3-x)2,解得x=1,即A′E=1;
同理在Rt△DCF中,设CF=x,根据勾股定理可求得x=1,即CF=1;
作EG⊥BF,则EG=AB=
 ,FG=AD-AE-CF=3-1-1=1,
,FG=AD-AE-CF=3-1-1=1,∴EF=
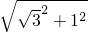 =2,
=2,∴四边形A′EFD的周长=1+
 +2+2=5+
+2+2=5+ .
.故答案为5

点评:本题除了用到了翻折变换外,还多次用到了勾股定理.在几何中勾股定理是常用的一个定理,所以学生一定要熟练掌握.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 将矩形纸片ABCD如图那样折叠,使顶点B与顶点D重合,折痕为EF.若AB=
将矩形纸片ABCD如图那样折叠,使顶点B与顶点D重合,折痕为EF.若AB= 将矩形纸片ABCD如图那样折叠,使顶点B与顶点D重合,折痕为EF.若AB=
将矩形纸片ABCD如图那样折叠,使顶点B与顶点D重合,折痕为EF.若AB=
 ,AD=3,则四边形A′EFD的周长为 .
,AD=3,则四边形A′EFD的周长为 .
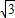 ,AD=3,则△DEF的周长为 .
,AD=3,则△DEF的周长为 .