题目内容
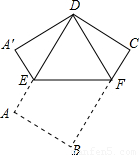
将矩形纸片ABCD如图那样折叠，使顶点B与顶点D重合，折痕为EF．若AB=| 3 |
分析：连接BD交EF于H点．
证∠A'DE=∠ADB=∠BDF=∠FDC=30°，根据角平分线上的点到角的两边的距离相等证EH=EA′，HF=FC．
证∠A'DE=∠ADB=∠BDF=∠FDC=30°，根据角平分线上的点到角的两边的距离相等证EH=EA′，HF=FC．
解答：
解：连接BD交EF于H点．
∵AB=
，AD=3，∴∠ADB=30°．
∵AD∥BC，FB=FD，∴∠ADB=∠DBF=∠BDF=30°．
∴∠A'DE=∠ADB=30°，∠BDF=∠FDC=30°．
∴EH=EA'=EA，FH=FC．
∴△DEF的周长为DE+EH+HF+DF=2AD=6．
解：连接BD交EF于H点．∵AB=
| 3 |
∵AD∥BC，FB=FD，∴∠ADB=∠DBF=∠BDF=30°．
∴∠A'DE=∠ADB=30°，∠BDF=∠FDC=30°．
∴EH=EA'=EA，FH=FC．
∴△DEF的周长为DE+EH+HF+DF=2AD=6．
点评：本题通过折叠变换考查学生的逻辑思维能力，解决此类问题，应结合题意，最好实际操作图形的折叠，易于找到图形间的关系．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
将矩形纸片ABCD如图那样折叠，使顶点B与顶点D重合，折痕为EF．若AB=
，AD=3，则四边形A′EFD的周长为 ．
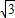，AD=3，则△DEF的周长为 ．