题目内容
如图，某飞机于空中探测某座山的高度，在点A处飞机的飞行高度是AF＝3700米，从飞机上观测山顶目标C的俯角是45°，飞机继续以相同的高度飞行300米到B处，此时观测目标C的俯角是50°，求这座山的高度CD．（参考数据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.20）．
解：设EC＝x．
在Rt△BCE中，tan∠EBC＝
，∴BE＝
＝
x．……………3分
在Rt△ACE中，tan∠EAC＝
，∴AE＝
＝x． ……………6分
∴300＋x＝x，∴x＝1800 ………………………………………………8分
∴山高CD＝DE－EC＝3700－1800＝1900（米）
答：这座山的高度是1900米．……………………………………………10分解析:
此题的关键是求出CE的长．可设CE为x千米，分别在Rt△ACE和Rt△BCE中，用x表示出AE、BE的长，根据AB=AE-BE=3即可求出CE的长；则CD=AF-EC，由此得解
在Rt△BCE中，tan∠EBC＝
，∴BE＝＝x．……………3分 在Rt△ACE中，tan∠EAC＝
，∴AE＝＝x． ……………6分∴300＋
x＝x，∴x＝1800 ………………………………………………8分∴山高CD＝DE－EC＝3700－1800＝1900（米）
答：这座山的高度是1900米．……………………………………………10分解析:
此题的关键是求出CE的长．可设CE为x千米，分别在Rt△ACE和Rt△BCE中，用x表示出AE、BE的长，根据AB=AE-BE=3即可求出CE的长；则CD=AF-EC，由此得解
练习册系列答案
相关题目
相同的高度飞行3千米到B处，此时观测目标C的俯角是60°，求此山的高度CD．（精确到0.1）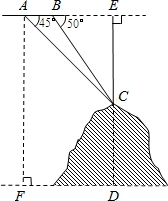
（2013•南通二模）如图，某飞机于空中探测某座山的高度，在点A处飞机的飞行高度是AF=3700米，从飞机上观测山顶目标C的俯角是45°，飞机继续以相同的高度飞行300米到B处，此时观测目标C的俯角是50°，求这座山的高度CD．
如图所示，某飞机于空中探测某座山的高度，此时飞机的飞行高度AF=4.5千米，从飞机上的A处测得观测山顶目标C的俯角是30°．飞机继续以相同的高度飞行4千米到B处，此时观测目标C的俯角为60°，求此山的高度CD（图中所有点在同一水平面内，结果精确到0.01千米）（参考数据：
