题目内容
如图,某飞机于空中探测某座山的高度.此时飞机的飞行高度是AF=3.7千米,从飞机上观测山顶目标C的俯视角为30°.飞机继续 相同的高度飞行3千米到B处,此时观测目标C的俯角是60°,求此山的高度CD.(精确到0.1)
相同的高度飞行3千米到B处,此时观测目标C的俯角是60°,求此山的高度CD.(精确到0.1)(参考数据:
| 2 |
| 3 |
分析:此题的关键是求出CE的长.可设CE为x千米,分别在Rt△ACE和Rt△BCE中,用x表示出AE、BE的长,根据AB=AE-BE=3即可求出CE的长;则CD=AF-EC,由此得解.
解答:解:设CE=x千米.
Rt△BCE中,∠CBE=60°,
∴BE=CE÷tan60°=
x.
Rt△ACE中,∠CAE=30°,
∴AE=EC÷tan30°=
x.
∴AB=AE-BE=
x=3,
解得x=
≈2.598.
∴CD=AF-CE=AF-x=3.7-2.598≈1.1(千米).
答:此山的高度约为1.1千米.
Rt△BCE中,∠CBE=60°,
∴BE=CE÷tan60°=
| ||
| 3 |
Rt△ACE中,∠CAE=30°,
∴AE=EC÷tan30°=
| 3 |
∴AB=AE-BE=
2
| ||
| 3 |
解得x=
3
| ||
| 2 |
∴CD=AF-CE=AF-x=3.7-2.598≈1.1(千米).
答:此山的高度约为1.1千米.
点评:本题考查俯角的定义,难点是能借助俯角构造直角三角形并利用相应的三角函数解直角三角形.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
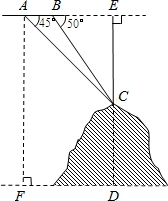 (2013•南通二模)如图,某飞机于空中探测某座山的高度,在点A处飞机的飞行高度是AF=3700米,从飞机上观测山顶目标C的俯角是45°,飞机继续以相同的高度飞行300米到B处,此时观测目标C的俯角是50°,求这座山的高度CD.
(2013•南通二模)如图,某飞机于空中探测某座山的高度,在点A处飞机的飞行高度是AF=3700米,从飞机上观测山顶目标C的俯角是45°,飞机继续以相同的高度飞行300米到B处,此时观测目标C的俯角是50°,求这座山的高度CD. 如图所示,某飞机于空中探测某座山的高度,此时飞机的飞行高度AF=4.5千米,从飞机上的A处测得观测山顶目标C的俯角是30°.飞机继续以相同的高度飞行4千米到B处,此时观测目标C的俯角为60°,求此山的高度CD(图中所有点在同一水平面内,结果精确到0.01千米)(参考数据:
如图所示,某飞机于空中探测某座山的高度,此时飞机的飞行高度AF=4.5千米,从飞机上的A处测得观测山顶目标C的俯角是30°.飞机继续以相同的高度飞行4千米到B处,此时观测目标C的俯角为60°,求此山的高度CD(图中所有点在同一水平面内,结果精确到0.01千米)(参考数据:
