题目内容
【题目】已知![]() 是等边三角形,
是等边三角形,![]() .
.
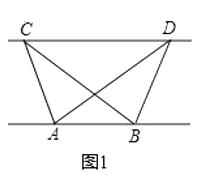
![]() 如图1,点E为BC上一点,点F为AC上一点,且
如图1,点E为BC上一点,点F为AC上一点,且![]() ,连接AE,BF交于点G,求
,连接AE,BF交于点G,求![]() 的度数;
的度数;
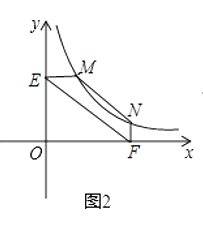
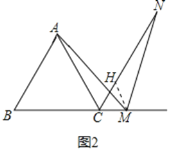
![]() 如图2,点M是BC延长线上一点,
如图2,点M是BC延长线上一点,![]() ,MN交
,MN交![]() 的外角平分线于点N,求
的外角平分线于点N,求![]() 的值;
的值;
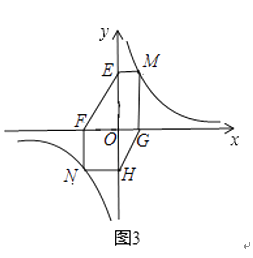
![]() 如图3,过点A作
如图3,过点A作![]() 于点D,点P是直线AD上一点,以CP为边,在CP的下方作等边
于点D,点P是直线AD上一点,以CP为边,在CP的下方作等边![]() ,连DQ,则DQ的最小值是______.
,连DQ,则DQ的最小值是______.

【答案】(1)60°;(2)6;(3)1.5.
【解析】
![]() 根据等边三角形的性质得到
根据等边三角形的性质得到![]() ,
,![]() ,证明
,证明![]() ≌
≌![]() ,根据全等三角形的性质,三角形的外角的性质计算,得到答案;
,根据全等三角形的性质,三角形的外角的性质计算,得到答案;![]() 作
作![]() 交CN于H,证明
交CN于H,证明![]() ≌
≌![]() ,根据全等三角形的性质得到
,根据全等三角形的性质得到![]() ,结合图形计算即可;
,结合图形计算即可;![]() 连接BQ,证明
连接BQ,证明![]() ≌
≌![]() ,得到
,得到![]() ,根据直角三角形的性质,垂线段最短解答即可.
,根据直角三角形的性质,垂线段最短解答即可.
![]() 为等边三角形,
为等边三角形,
![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,
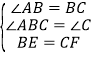 ,
,
![]() ≌
≌![]()
![]() ,
,
![]() ,
,
![]() ;
;
![]() 如图2,作
如图2,作![]() 交CN于H,
交CN于H,
![]() ,
,
![]() 是
是![]() 的外角平分线,
的外角平分线,
![]() ,
,
![]() 为等边三角形,
为等边三角形,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
![]() ≌
≌![]()
![]() ,
,
![]() ;
;
![]() 连接BQ,
连接BQ,
![]() 是等边三角形,
是等边三角形,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() 是等边三角形,
是等边三角形,
![]() ,
,![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,
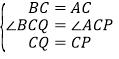 ,
,
![]() ≌
≌![]()
![]() ,
,
当![]() 时,DQ最小,最小值为
时,DQ最小,最小值为![]() ,
,
故答案为:![]() .
.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
【题目】某同学在用描点法画二次函数y= ![]() +bx+c的图象时,列出了下面的表格:
+bx+c的图象时,列出了下面的表格:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | ﹣11 | ﹣2 | 1 | ﹣2 | ﹣5 | … |
由于粗心,他算错了其中一个y值,则这个错误的数值是( ).
A.﹣11 B.﹣2 C.1 D.﹣5