Question

【题目】平面直角坐标系中，点、、，…和、、，…分别在直线和轴上．，，，…都是等腰直角三角形，如果，，则点的横坐标是_________

Answer 1

【答案】766

【解析】

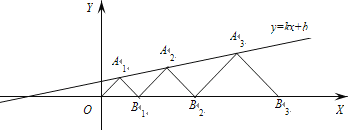
利用待定系数法可得A1、A2、A3的坐标，进而得出各点的坐标的规律．

解：因为三角形都是等腰直角三角形，所以设A1（m，m），则有m=m+，解得m=1，
∴A1（1，1），
设A2（2+n，n），则n=（n+2）+，
解得n=2，
∴A2（4，2），
设A3（6+a，a），则有a=（6+a）+，
解得a=4，
∴A3（10，4），
由此发现点An的纵坐标为2n-1，又∵点An在直线上，
∴点An的横坐标是3×2n-1-2,

∵n=9, ∴An的横坐标是3× -2=766.

故答案为:766．