题目内容
18.已知m<n,那么下列各式中,不一定成立的是( )| A. | 3m<3n | B. | 2-m>2-n | C. | mc2<nc2 | D. | m-3<n-2 |
分析 由基本不等式m<n,根据不等式的性质,逐一判断.
解答 解:A、由m<n,根据不等式性质2,得3m<3n,不符合题意;
B、由m<n,根据不等式性质3,得-m>-n,再根据不等式性质1,得2-m>2-n,不符合题意;
C、因为c2≥0,当c2>0时,根据不等式性质2,得mc2<nc2,当c2=0时,mc2=nc2,符合题意;
D、由m<n,根据不等式性质1,得m-3<n-3<n-2,不符合题意.
故选C.
点评 本题考查了不等式的性质.不等式的基本性质:
(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.
(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.
(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8. 如图,下列条件中,能够判定AB∥CD的是( )
如图,下列条件中,能够判定AB∥CD的是( )
 如图,下列条件中,能够判定AB∥CD的是( )
如图,下列条件中,能够判定AB∥CD的是( )| A. | ∠2=∠4 | B. | ∠1=∠2+∠3 | C. | ∠3=∠5 | D. | ∠D+∠4+∠5=180° |
9.下列说法正确的个数是( )
①1$\frac{2}{3}$的倒数是$\frac{5}{2}$;
②3$\frac{1}{4}$不能化成有限小数;
③扇形的面积计算公式是S=$\frac{1}{2}$lr;
④扇形的弧长公式是l=$\frac{n}{180}$•2πr.
①1$\frac{2}{3}$的倒数是$\frac{5}{2}$;
②3$\frac{1}{4}$不能化成有限小数;
③扇形的面积计算公式是S=$\frac{1}{2}$lr;
④扇形的弧长公式是l=$\frac{n}{180}$•2πr.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.如图,已知△ABC的六个元素,那么甲、乙、丙三个三角形中和△ABC全等的三角形是( )


| A. | 甲和乙 | B. | 甲和丙 | C. | 只有甲 | D. | 只有丙 |
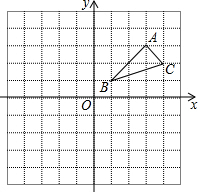 如图在平面直角坐标系中,每个小方格是边长为1的正方形,已知△ABC.
如图在平面直角坐标系中,每个小方格是边长为1的正方形,已知△ABC. 如图,点A在点O北偏东32°方向上,点B在点O南偏东43°方向上,则∠AOB=105°.
如图,点A在点O北偏东32°方向上,点B在点O南偏东43°方向上,则∠AOB=105°.