题目内容
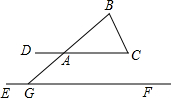 如图,已知DC∥EF,点A在DC上,BA的延长线交EF于点G,AB=AC,∠AGE=130°,则∠B的度数是
如图,已知DC∥EF,点A在DC上,BA的延长线交EF于点G,AB=AC,∠AGE=130°,则∠B的度数是
- A.50°
- B.65°
- C.75°
- D.55°
B
分析:先根据平行线的性质求得∠DAB的度数,再根据三角形的外角性质和等腰三角形的性质求得∠B的度数.
解答:∵DC∥EF,∠AGE=130°,
∴∠DAB=130°,
∵AB=AC,
∴∠B=∠C,
∵∠DAB=∠B+∠C,
∴∠B=65°.
故选B.
点评:综合考查了平行线的性质,三角形的外角性质和等腰三角形的性质.
分析:先根据平行线的性质求得∠DAB的度数,再根据三角形的外角性质和等腰三角形的性质求得∠B的度数.
解答:∵DC∥EF,∠AGE=130°,
∴∠DAB=130°,
∵AB=AC,
∴∠B=∠C,
∵∠DAB=∠B+∠C,
∴∠B=65°.
故选B.
点评:综合考查了平行线的性质,三角形的外角性质和等腰三角形的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,已知DC∥EF,点A在DC上,BA的延长线交EF于点G,AB=AC,∠AGE=130°,则∠B的度数是( )
如图,已知DC∥EF,点A在DC上,BA的延长线交EF于点G,AB=AC,∠AGE=130°,则∠B的度数是( ) 如图,已知BC∥EF,BC=EF,AF=DC.则AB=DE.在相应序号内说明理由.
如图,已知BC∥EF,BC=EF,AF=DC.则AB=DE.在相应序号内说明理由.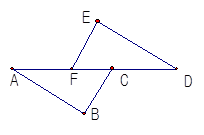
 BC=EF( 已知 )
BC=EF( 已知 )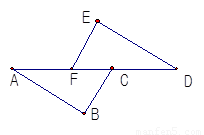
 BC=EF( 已知 )
BC=EF( 已知 )