题目内容
如图，为测量小区内池塘最宽处A、B两点间的距离，在池塘边定一点C，使∠BAC=90°，并测得AC的长18m，BC的长为30m，则最宽处AB的距离为
- A.18m
- B.20m
- C.22m
- D.24m
D
分析：根据题意可以得到三角形ABC为直角三角形，用勾股定理求得AB的长即可．
解答：∵∠BAC=90°，并测得AC的长18m，BC的长为30m，
∴由勾股定理得：AB=
=
=24m，
故选D．
点评：本题考查了勾股定理的应用，解题的关键是从实际问题中整理出直角三角形并利用勾股定理求解．
分析：根据题意可以得到三角形ABC为直角三角形，用勾股定理求得AB的长即可．
解答：∵∠BAC=90°，并测得AC的长18m，BC的长为30m，
∴由勾股定理得：AB=
==24m，故选D．
点评：本题考查了勾股定理的应用，解题的关键是从实际问题中整理出直角三角形并利用勾股定理求解．
练习册系列答案
相关题目
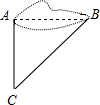如图，为测量小区内池塘最宽处A、B两点间的距离，在池塘边定一点C，使∠BAC=90°，并测得AC的长18m，BC的长为30m，则最宽处AB的距离为（ ）| A、18m | B、20m | C、22m | D、24m |
如图，为测量小区内池塘最宽处A、B两点间的距离，在池塘边定一点C，使∠BAC=90°，并测得AC的长30m，BC的长为50m，则最宽处AB的距离为（ ）
如图，为测量小区内池塘最宽处A、B两点间的距离，在池塘边定一点C，使∠BAC=90°，并测得AC的长30m，BC的长为50m，则最宽处AB的距离为