题目内容
如图(15-1),点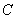 将线段
将线段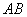 分成两部分,如果
分成两部分,如果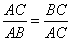 ,那么称点
,那么称点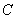 为线段
为线段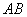 的黄金分割点。某数学兴趣小组在进行课题研究时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线
的黄金分割点。某数学兴趣小组在进行课题研究时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线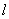 将一个面积为
将一个面积为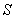 的图形分成两部分,这两部分的面积分别为
的图形分成两部分,这两部分的面积分别为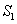 、
、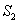 ,如果
,如果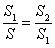 ,那么称直线
,那么称直线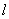 为该图形的黄金分割线.
为该图形的黄金分割线.
(1)如图(15-2),在△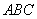 中,
中,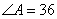 °,
°,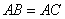 ,
, 的平分线交
的平分线交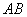 于点
于点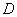 ,请问点
,请问点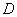 是否是
是否是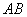 边上的黄金分割点,并证明你的结论;
边上的黄金分割点,并证明你的结论;
(2)若△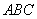 在(1)的条件下,如图(15-3),请问直线
在(1)的条件下,如图(15-3),请问直线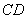 是不是△
是不是△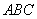 的黄金分割线,并证明你的结论;
的黄金分割线,并证明你的结论;
(3)如图(15-4),在直角梯形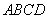 中,
中,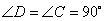 ,对角线
,对角线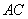 、
、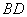 交于点
交于点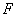 ,延长
,延长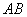 、
、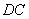 交于点
交于点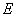 ,连接
,连接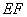 交梯形上、下底于
交梯形上、下底于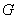 、
、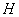 两点,请问直线
两点,请问直线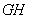 是不是直角梯形
是不是直角梯形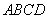 的黄金分割线,并证明你的结论.
的黄金分割线,并证明你的结论.
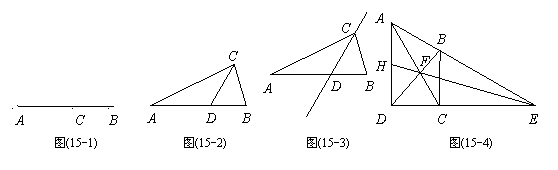

解:(1)点D是AB边上的黄金分割点.理由如下:
由题易证△BCD∽△BAC,得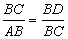 ,
,
∴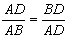 ,
,
∴点D是AB边上的黄金分割点. …
(2)直线CD是△ABC的黄金分割线.理由如下:
设△ABC中,AB边上的高为h,
则S△ABC=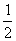 AB•h,S△ACD=
AB•h,S△ACD=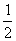 AD•h,S△BCD=
AD•h,S△BCD=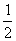 BD•h.
BD•h.
∴S△ACD:S△ABC=AD:AB,S△BCD:S△ACD=BD:AD.
由(1)知,点D是AB边上的黄金分割点,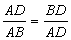
∴S△ACD:S△ABC=S△BCD:S△ACD ,
,
∴CD是△ABC的黄金分割线.
(3)直线不是直角梯形ABCD的黄金分割线.理由如下:
∵BC∥AD,
∴△EBG∽△EAH,△EGC∽△EHD,
∴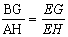 ,
,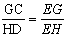 ,
,
∴ ,即
,即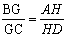 ①
①
同理,由△BGF∽△DHF,△CGF∽△AHF得:
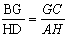 ,即
,即 ②
②
由①、②得: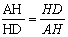
∴AH=HD,
∴BG=GC.
∴梯形ABGH与梯形GCDH上下底分别相等,高也相等,
∴S梯形ABGH=S梯形GCDH=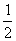 S梯形ABCD.
S梯形ABCD.
∴GH不是直角梯形ABCD的黄金分割线.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
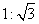 ,BD的坡比
,BD的坡比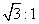 AB=10m.请你根据以上数据计算GH的长.
AB=10m.请你根据以上数据计算GH的长.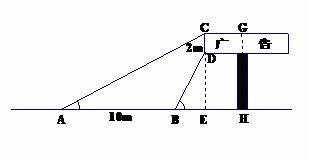
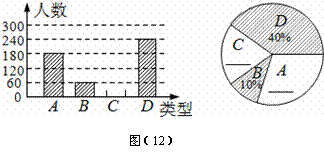
 =
= 
 (B) 等腰梯形
(B) 等腰梯形 C.
C.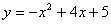 与x轴交于A、B两点,与
与x轴交于A、B两点,与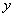 轴交于点C.已知M(0,1),E(a,0),F(a+1,0),点P是第一象限内的抛物线上的动点.△PCM是以CM为底的等腰三角形,则点P的坐标为_________;当a=______时
轴交于点C.已知M(0,1),E(a,0),F(a+1,0),点P是第一象限内的抛物线上的动点.△PCM是以CM为底的等腰三角形,则点P的坐标为_________;当a=______时 ,四边形PMEF周长最小.
,四边形PMEF周长最小.