题目内容
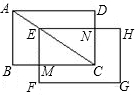如图，ABCD与EFGH是两个全等的矩形，对应边互相平行，点E在AC上，已知AD=8，AB=6，两矩形的公共部分EMCN的面积是矩形ABCD面积的一半，则AE的长是________．
10-5
分析：根据公共部分EMCN的面积是矩形ABCD的面积的一半，可得CM•CN=
BC•CD，且对应边互相平行，则
=
，即可求得CM、CN的值．
解答：∵AD=8，CD=6，∴AC=
=10，
∵公共部分EMCN的面积是矩形ABCD的面积的一半，
∴CM•CN=BC•CD，
ABCD与EFGH的对应边互相平行，
∴=，
∴CM=
BC，CN=CD，
∴CM=4，CN=3，
∴CE=
=5，
∴AE=AC-CE=10-5，
故答案为 10-5．
点评：本题考查了勾股定理在直角三角形中的运用，考查了矩形面积的计算，本题中正确计算CE的长是解题的关键．
分析：根据公共部分EMCN的面积是矩形ABCD的面积的一半，可得CM•CN=
BC•CD，且对应边互相平行，则=，即可求得CM、CN的值．解答：∵AD=8，CD=6，∴AC=
=10，∵公共部分EMCN的面积是矩形ABCD的面积的一半，
∴CM•CN=
BC•CD，ABCD与EFGH的对应边互相平行，
∴
=，∴CM=
BC，CN=CD，∴CM=4
，CN=3，∴CE=
=5，∴AE=AC-CE=10-5
，故答案为 10-5
．点评：本题考查了勾股定理在直角三角形中的运用，考查了矩形面积的计算，本题中正确计算CE的长是解题的关键．
练习册系列答案
相关题目
47、如图，?ABCD的对角线相交于点O，EF过点O分别与AD，BC相交于点E，F．若AB=4，BC=7，OE=3，则四边形EFCD的周长为
22、如图，ABCD是正方形，P是对角线BD上一点，过P点作直线EF、GH分别平行于AB、BC，交两组对边于E、F、G、H，则四边形PEDG，四边形PHBF都是正方形，四边形PEAH、四边形PGCF都是矩形，设正方形PEDG的边长是a，正方形PHBF的边长是b． 请动手实践并得出结论：
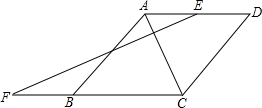如图菱形ABCD中，点E是AD的中点，EF⊥AC交CB的延长线于点F，交AC于点M，想一想：AB与EF是否互相平分，并说明理由．
如图，ABCD是正方形，M是BC中点，将正方形折起，使点A与点M重合，设折痕为EF，若正方形面积是64，那么梯形AEFD的面积是