题目内容
 如图,ABCD是正方形,M是BC中点,将正方形折起,使点A与点M重合,设折痕为EF,若正方形面积是64,那么梯形AEFD的面积是
如图,ABCD是正方形,M是BC中点,将正方形折起,使点A与点M重合,设折痕为EF,若正方形面积是64,那么梯形AEFD的面积是24
24
.分析:正方形面积是64,则边长为8;设AE=x,由折叠可知EM=AE=x,BE=8-x,BM=8÷2=4,在Rt△BME中,运用勾股定理求x;设DF=y,CF=8-y,AF=FM,利用勾股定理即可求出y;以AE和DF为底,AD为高计算梯形AEFD的面积.
解答:解:依题意得,正方形的边长为8,设AE=x,
由折叠可知EM=AE=x,BE=8-x,BM=8÷2=4,
在Rt△BME中,BE2+BM2=EM2,即(8-x)2+42=x2,
解得:x=5,
再设DF=y,则CF=8-y,
AD2+DF2=CF2+CM2,即82+y2=(8-y)2+42,
解得:y=1,
S梯形AEFD=
×(AE+DF)×AD=
×(5+1)×8=24.
故答案为:24.
由折叠可知EM=AE=x,BE=8-x,BM=8÷2=4,
在Rt△BME中,BE2+BM2=EM2,即(8-x)2+42=x2,
解得:x=5,
再设DF=y,则CF=8-y,
AD2+DF2=CF2+CM2,即82+y2=(8-y)2+42,
解得:y=1,
S梯形AEFD=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:24.
点评:本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后角相等.

练习册系列答案
相关题目
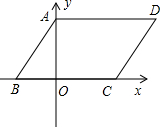 x2-7x+12=0的两个根,且OA>OB.
x2-7x+12=0的两个根,且OA>OB.

