题目内容
如图,对称轴为直线x=2的抛物线经过点A(-1,0),C(0,5)两点,与x轴另一交点为B,已知M(0,1),E(a,0),F(a+1,0),点P是第一象限内的抛物线上的动点.
(1)求此抛物线的解析式;
(2)当a=1时,求四边形MEFP面积的最大值,并求此时点P的坐标;
(3)若△PCM是以点P为顶点的等腰三角形,求a为何值时,四边形PMEF周长最小?请说明理由.

(1)y=-x2+4x+5;(2)当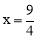 时,四边形MEFP面积的最大,最大值为
时,四边形MEFP面积的最大,最大值为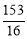 ,此时点P坐标为
,此时点P坐标为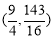 ;(3)当
;(3)当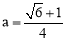 时,四边形FMEF周长最小.
时,四边形FMEF周长最小.
【解析】
试题分析:(1)设顶点式,利用待定系数法求出抛物线的解析式.
(2)求出四边形MEFP面积的表达式,利用二次函数的性质求出最值及点P坐标.
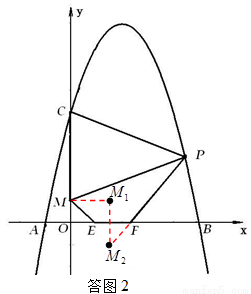
(3)四边形PMEF的四条边中,PM、EF长度固定,因此只要ME+PF最小,则PMEF的周长将取得最小值.如答图2所示,将点M向右平移1个单位长度(EF的长度),得M1(1,1);作点M1关于x轴的对称点M2,则M2(1,﹣1);连接PM2,与x轴交于F点,此时ME+PF=PM2最小.
试题解析:【解析】
(1)∵抛物线的对称轴为直线x=2,∴设抛物线为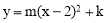 .
.
∵抛物线过点A(-1,0)、C(0,5),
∴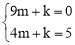 ,解得:
,解得: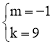 .
.
∴二次函数的函数关系式为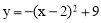 ,即y=-x2+4x+5.
,即y=-x2+4x+5.
(2)当a=1时,E(1,0),F(2,0),
设P的坐标为(x,-x2+4x+5)
如答图1,过点P作y轴的垂线,垂足为G,
则四边形MEFP面积
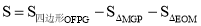 =
=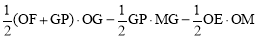
=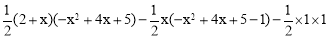 =
=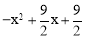 =
=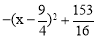 ,
,
∴当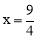 时,四边形MEFP面积的最大,最大值为
时,四边形MEFP面积的最大,最大值为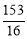 ,此时点P坐标为
,此时点P坐标为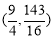 .
.
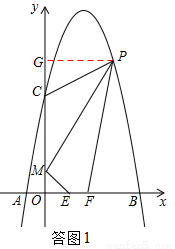
(3)如答图2,把点M向右平移1个单位得点M1,再做点M1关于x轴的对称点M2,在四边形FMEF中,因为边PM,EF为固定值,所以要使四边形FMEF周长最小,则ME+PF最小,因为ME=M1F=M2F,所以只要使M2F+PF最小即可,所以点F应该是直线M2P与x轴的交点,由OM=1,OC=5,得点P的纵坐标为3,根据y=-x2+4x+5可求得点P(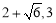 )
)
又点M2坐标为(1,-1),∴直线M2P的解析式为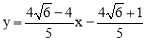 .
.
当y=0时,求得 ,∴F(
,∴F(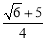 ,0).∴
,0).∴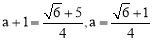 .
.


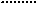 ∴当
∴当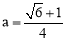 时,四边形FMEF周长最小.
时,四边形FMEF周长最小.
考点:1. 二次函数综合题;2.单动点问题;3.待定系数法的应用;4.曲线上点的坐标与方程的关系;5.二次函数的性质;6.由实际问题列函数关系式;7.等腰三角形的性质;8.轴对称的应用(最短线路问题).

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 B.
B. C.
C. D.
D.
 (x>0)于点C1,C2,…,Cn﹣1.若C15B15=16C15A15,则n的值为 .(n为正整数)
(x>0)于点C1,C2,…,Cn﹣1.若C15B15=16C15A15,则n的值为 .(n为正整数)
 cm B.
cm B.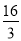 cm C.
cm C. cm D.
cm D. cm
cm